
«دقت ریاضی بسیار زیاد در فیزیک استفاده چندانی ندارد. اما کسی نباید از ریاضیدانها در این باره اشکالی بگیرد […] آنها دارند کار خودشان را انجام میدهند.»
از دید بسیاری از فیزیکدانها، دقت ریاضی (mathematical rigor) در اکثر اوقات برای جامعه فیزیک غیرضروری بوده و حتی با کند کردن سرعت پیشرفت فیزیک میتواند برای آن مضر نیز باشد.
شاید بتوان دلیل فاینمن را برای بیان این نظر درک کرد؛ برای لحظهای تصور کنید که فاینمن فرمالیسم انتگرال مسیر خود را به دلیل وجود نداشتن تعریف دقیق ریاضی از این انتگرالهای واگرا (که تا به امروز نیز تعریف جامع و دقیقی از آنها در دسترس نیست) معرفی نمیکرد و یا فیزیکدانها به دلیل وجود نداشتن تعریف اصول موضوعهای از نظریه میدانهای کوانتومی، از آن استفاده نمیکردند! قطعا انتظار سطح یکسانی از دقت ریاضی در اثبات قضایای ریاضی و در نظریههای فیزیکی انتظاری بیش از حد سنگین و غیر عملی است اما، بر خلاف برداشت رایج در بین فیزیکدانها، دقت ریاضی همیشه به معنی جایگزین کردن استدلالهای بدیهی اما غیر دقیق با اثباتهای خسته کننده نیست. در بیشتر اوقات دقت ریاضی به معنی مشخص کردن تعریفهای دقیق و واضح برای اجزای یک نظریه است به طوری که استدلالهای منطبق بر شهود با قطعیت درست هم باشند! شاید بتوان این مطلب را در نقل قول زیر خلاصه کرد:
«دقت ریاضی پنجرهای را غبارروبی میکند که نور شهود از طریق آن به داخل میتابد.»
اِلیس کوپر
در فرمولبندی نظریههای فیزیکی، بیتوجهی به پیشفرضها و ظرافتهای ریاضی میتواند به سادگی به نتایجی در ظاهر متناقض بیانجامد که در بسیاری از موارد عجیب و حیرتانگیز به نظر میرسند. این مثال ساده از مکانیک کوانتومی را در نظر بگیرید: برای ذرهای کوانتومی در یک بعد، عملگرهای تکانه خطی P و مکان Q از رابطه جابهجایی هایزنبرگ پیروی میکنند
حال با گرفتن رد (trace) از دو طرف این رابطه مشاهده میکنیم که رد طرف چپ این معادله با استفاده از خاصیت جابهجایی عمل ردگیری صفر میشود در حالی که رد سمت راست این معادله غیر صفر است! از آنجا که این رابطه یکی از بنیادینترین روابط مکانیک کوانتومی است و بسیاری از مفاهیم عمیق فیزیکی مکانیک کوانتوم نظیر اصل عدم قطعیت از آن نتیجه میشود، این نتیجه (به ظاهر) متناقض حیرت انگیز به نظر میرسد! برای پیدا کردن مشکل بیاید نگاه دقیقتری به رابطه جابهجایی هایزنبرگ و دامنه اعتبار تعریف عمل ردگیری بیاندازیم: فرض کنید رابطه جابهجایی بالا برای دو عملگر P و Q، که روی فضای هیلبرت H با بعد متناهی n تعریف میشوند، برقرار باشد. در این صورت، عملگرهای P و Q با ماتریسهای n*n مختلط داده خواهند شد و عمل ردگیری از آنها خوشتعریف است. بنابرین، نتیجه متناقض
نشان میدهد که رابطه جابهجایی هایزنبرگ نمیتواند روی فضاهای هیلبرت با بعد متناهی برقرار باشد. در نتیجه مکانیک کوانتومی باید روی فضای هیلبرت با بعد نامتناهی (اما شمارا) تعریف شود: روی چنین فضاهایی عمل ردگیری برای تمام عملگرها خوشتعریف نبوده (به طور مشخص رد عملگر واحد روی این فضاها تعریف نشده است) و نمیتوان تناقض بالا را روی این دسته از فضاها نتیجهگیری کرد! با تعمیم تناقض بالا به فضاهای هیلبرت بینهایت بعدی حتی میتوان نتیجه قویتری نیز درباره عملگرهای تکانه و مکان گرفت ــ حداقل یکی از این عملگرها باید بیکران (unbounded) باشد؛ این بدان معنی است که مقادیر ویژه کراندار نبوده و این عملگر روی تمام فضای هیلبرت خوشتعریف نخواهد بود! این نتیجه خود به آن معنی است که نه عملگرهای خلق و فنا و نه عملگر هامیلتونی (انرژی) روی تمام حالات فضای هیلبرت نوسانگر هماهنگ خوشتعریف نیستند (هر چند میتوان بستار این عملگرها را روی کل فضای هیلبرت تعریف نمود). هر کدام از این نتایج خود منجر به نتیجهگیریهای شگفتانگیز دیگری میشوند که ما را مجبور میسازند در تعریف بسیاری از مفاهیم به نظر بدیهی تجدید نظر کنیم: برای مثال، در فضاهای هیلبرت بینهایت بعدی و در حالتی که تمام عملگرهای فیزیکی کراندار باشند، میتوان حالتی را متصور شد که فضا هیلبرت شامل هیچ حالت غیر درهمتنیدهای بین دو «زیر سیستم» نباشد و در نتیجه نتوان آن را به صورت ضرب تانسوری دو فضای هیلبرت متعلق به هر زیر سیستم نوشت! این مسئله نیاز به تعریف دقیقتری از مفهوم «زیر سیستم» در نظریه میدانهای کوانتومی و تعمیمهای آن (مانند نظریه گرانش کوانتومی) را نشان میدهد که خود میتواند به حل شدن بخشی از تناقضهای عمیقتر مانند مسئله اطلاعات سیاهچالهها منجر شود! توجه کنید که دقت به دامنه اعتبار رابطه جابهجایی هایزنبرگ به نوبه خود چگونه میتواند ما را در درک بهتر درهمتنیدگی در نظریه میدانهای کوانتومی و سوالاتی عمیقتر از جمله ساختار علی فضا و زمان و یا مسئله اطلاعات سیاهچالهها یاری کند! مثالهایی از این دست در مکانیک کوانتومی و نظریه میدانهای کوانتومی به فراوانی یافت میشوند که چند مثال دیگر و توضیح مفصل در مورد چگونگی حل آنها را میتوانید در مقاله آموزشی (و بسیار هیجانانگیز) زیر پیدا کنید:
Mathematical surprises and Dirac’s formalism in quantum mechanics
François Gieres 2000 Rep. Prog. Phys. 63 1893
By a series of simple examples, we illustrate how the lack of mathematical concern can readily lead to surprising mathematical contradictions in wave mechanics. The basic mathematical notions allowing for a precise formulation of the theory are then summarized and it is shown how they lead to an elucidation and deeper understanding of the aforementioned problems. After stressing the equivalence between wave mechanics and the other formulations of quantum mechanics, i.e. matrix mechanics and Dirac’s abstract Hilbert space formulation, we devote the second part of our paper to the latter approach: we discuss the problems and shortcomings of this formalism as well as those of the bra and ket notation introduced by Dirac in this context. In conclusion, we indicate how all of these problems can be solved or at least avoided.
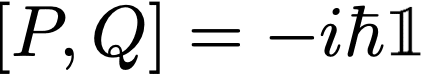

[…] ریاضی (محاسبات قلم و کاغذی و کامپیوتری) ممکنه. مثلا این نوشته رو […]