فرکتال‌ها| قسمت چهارم، مجموعه‌ی ژولیا

در قسمت‌های قبل در مورد فرکتال‌ها و ویژگی‌هاشون نوشتم. این قسمت و قسمت بعد در مورد مجموعه‌ای از اعداد که اشکال فرکتالی می‌سازند هست.

به عنوان مقدمه،‌ تابع 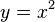رو در نظر بگیرید. اگر به عنوان یک نقطه‌ی شروع x=۲ رو به تابع بدیم مقدار تابع میشه ۲ به توان ۲ یعنی ۴. حالا اگر باز این ۴ رو به تابع بدیم، جواب ۱۶ میشه و اگر این روند رو ادامه بدیم به عددهای بزرگتر می‌رسیم. همین طور اگر از نقطه‌ی x=-۳ شروع کنیم، به ۹ و بعد از اون به ۸۱ و مجددا به عددهای بزرگتری می‌رسیم.

نقطه‌ی شروع:۲          ۲ => ۴ =>  ۱۶=>۲۵۶ => … => بی‌نهایت

نقطه‌ی شروع: ۳-         ۳- => ۹ => ۸۱=>۶۵۶۱ => … => بی‌نهایت

هر دوی این نقاط بعد از تکرارهای پی در پی به بی‌نهایت نزدیک میشند. اما اگر این بار یک نقطه از بازه‌ی [۱،۱-] انتخاب کنیم چی؟ مثلا اگر ۰/۵ رو انتخاب کنیم به توان دو که برسه میشه ۲۵/. بعدش ۶۲۵./. و همین طور عددهای بعدی کوچیک و کوچیکتر میشند و به صفر میل کنند.

نقطه‌ی شروع: ۵/.          ۵/. => ۲۵/. => ۶۲۵./.=> ۰۰۳۹۰۶۲۵/. => … => صفر

نقطه‌ی شروع:۱ یا ۱-          ۱یا ۱- => ۱ =>  ۱=>۱ => … => ۱

در حقیقیت هر عددی که انتخاب کنیم در نهایت (پس از تکرارهای پی در پی) سرانجام و عاقبتش دو حالت داره؛ یا خیلی رشد میکنه و به یک حد بی کران می‌رسه یا اینکه در آخر به یک مقدار ثابت همگرا میشه که برای این تابع اعداد ۱ و ۱- به ۱ همگرا میشند و همه‌ی اعداد حقیقی بین ۱- و ۱ به صفر. اعداد خارج این بازه هم که اصلا همگرا نمیشند!

خب بعد از این مقدمه، به یک تعریف می‌رسیم: «به مجموعه‌ای از شرایط اولیه که پس از تکرارهای پی‌در‌پی توسط یک تابع به بی‌نهایت میل نمی‌کنند، مجموعه‌ی ژولیای آن تابع می‌گویند.» مثلا برای تابع 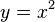  شرایط اولیه (اعداد) عضو بازه‌ی [۱،۱-] پس از تکرارهای پی‌در‌پی به بی‌نهایت نمی‌رسند ولی برای خارج از این بازه این طور نیست و همون جوری که دیدید بعد از تکرارهای پی‌در‌پی به بی‌نهایت می‌رسند. در حقیقت به مجموعه [۱،۱-]=S یک «مجموعه‌ی توپور ژولیا» میگند و منظور از مجموعه ژولیا مرز بین دو مجموعه است؛مجموعه شرایط اولیه‌ای که به بی‌نهایت می‌رسند و مجموعه شرایط اولیه‌ای که به بی‌نهایت نمی‌رسند! یعنی برای تابع  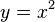 مجموعه ژولیا {J ={-1,1 است که شامل دو عدد ۱+ و ۱- می‌باشد! به عبارت دیگه اگر روی محور xها بخواییم مشخص کنیم فقط دو تا نقطه به عنوان مجموعه‌ی ژولیا تابع  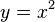 مشخص میشه؛ x=1 و x= -1!

خب تا اینجا زیاد جذاب نبود و فقط یک تعریف رو مطرح کردیم! حالا برای ایجاد جذابیت بیایید و وارد اعداد موهومی بشیم. تفاوت اعداد حقیقی و موهومی در اینه که اعداد حقیقی روی یک خط هستند ولی اعداد موهومی روی یک صفحه قرار می‌گیرند. هر عدد موهومی به صورت z=a+ib نوشته میشه که a, b هر دو اعداد حقیقی و i واحد موهومی ساز هست جوری که طبق تعریف: i² = −1 ! اگر با این دسته از اعداد هنوز آشنایی ندارید، سخت نگیرید، ایده‌ی آسونیه، می‌تونید نگاه کنید به صفحه ویکی‌پدیا یا اینکه اگر اشتیاق بیشتری به یادگیری دارید بهتون پیشنهاد میکنم کتاب «متغیرهای موهومی و کاربردها» نوشته‌ی جیمز براون و روئل چرچیل رو یه نگاهی بندازید! الان همون تابع قبلی رو در فضای موهومی می‌نویسیم:

در مورد این تابع، مجموعه‌ی ژولیا، مجموعه نقاطی هست که روی دایره‌ای به شعاع ۱ و به مرکز مبدا مختصات قرار می‌گیرند. یعنی مجموعه نقاط روی دایره و درون دایره r=1 مجموعه‌ی توپور ژولیا رو می‌سازند. این به خاطر اینه که اعداد موهومی روی صفحه مشخص می‌شند. (شما این تعبیر رو با نوشتن صورت قطبی اعداد موهومی بهترین می‌تونید ببینید؛ یادتون باشه که ما دنبال اعدادی هستیم که (z) عضو بازه‌ی [۱،۱-] باشند تا بعد از تکرارهای پی‌در‌پی، اعداد حاصل از به توان ۲ رسوندن به بی‌نهایت میل نکنند! صرفا جهت یادآوری عرض کنم که برای به توان رسوندن یک عدد موهومی z=a+ib مثل به توان رسوندن چند جمله‌ای ها عمل می‌کنیم ولی به این نکته توجه می‌کنیم که طبق تعریف i² = −1 !)

خب یکمی جالب‌تر شد، از دو نقطه‌ی x=1 و x= -1 توی قسمت قبل این دفعه به یک دایره رسیدیم در فضای موهومی. برای جذابیت بیشتر بیایید و این دفعه تابع رو تغییر بدیم و از این تابع استفاده کنیم و ببینیم که چی میشه! یعنی اون نقاطی رو پیدا کنیم که بعد از تکرارهای متوالی توسط این تابع به بی‌نهایت میل نکنند. راستش این دفعه به سادگی دفعه‌ی قبل نیست که بتونیم سریع کل اون اعداد رو حدس بزنیم و مثلا بگیم که ما دنبال اعدادی هستیم که (z) عضو بازه‌ی [۱،۱-] باشند. خب بیایید و چند تا عدد موهومی رو تست کنیم، روش آزمون و خطا؛
چندتا عدد راحت مثل 0 و i و 1+i و یک عدد یکمی ناراحت ( 😀 ) مثل 0.8 + 0.2i

می‌‌بینیم که صفر به طور متناوب به ۱- و صفر میرسه ولی در مورد بقیه اعداد ما، این طوری نیست و مثلا در مورد 1+i همین طور زیاد و زیاد تر میشه.

خب بقیه اعداد رو باید همین جوری با آزمون و خطا پیدا کرد راستش و خب این قدری رنج آوره! اشکال نداره ما خودمون این کارو انجام نمی‌دیم و میذاریم کامپیوتر بقیه اعداد رو پیدا کنه! من تصویری از نقاطی که مشخص شده رو براتون می‌‌‌ذارم تا ببینید که این دفعه شکل دیگه دایره نمیشه و یه شکل عجیب درست میشه! فکر نمی‌کنم که این شکل رو می‌شد به این راحتی‌ها حدس زد! برای بهتر دیده شدن تصویر، رزولوشنش رو میشه بیشتر کرد،یعنی تعداد نقاط رو بیشتری رو امتحان کرد:

«این یک شکل خودمتشابه هست!»

اجازه بدید تا یک قسمت از شکل که مشخص کردم رو بزرگترش کنم؛ مثل اینکه سر و کله‌ی فرکتال  ها دوباره پیدا شد!

از حالا به بعد هر تابعی که داشته باشیم رو می‌تونیم مجموعه‌ی ژولیا مربوط به اون رو پیدا کنیم.بین توابع، توابعی که به صورت چندجمله‌ای های مربعی هستند بیشتر معروف هستند!

$$ f(z)=z^2 +c ,$$  c:مقدار ثابت

حتما به صفحه‌ی ویکی‌پدیا مجموعه‌ی ژولیا سر بزنید و شکل‌های جالبی که توسط توابع مختلف ساخته شده رو ببینید. علت استفاده از رنگ هم اینه: بسته به این که نقاط با چه آهنگی رشد می‌کنند به اونها یک رنگ خاص اختصاص میدند، ممکنه یک عدد بعد از صد بار تکرار بیشتر از یک میلیون بشه و یک عدد بعد از هزار بار تکرار، این‌ها باید با هم یک فرقی به هر حال داشته باشند دیگه! به عنوان نمونه من چند تا از تصاویر رو میذارم:

مجموعه‌ی ژولیا با رنگ سفید مشخص شده.

این نوشته را برای جزئیات بیشتر و تخصصی‌تر بخوانید:

The Beauty of Roots