چهارسال گذشت و دوره کارشناسی فیزیک من تموم شد. چهارسال پر از فراز و نشیبی که با تمام لذتها و هیجانها، سختیها و فشارها بالاخره به پایان رسید (من ورودی ۹۱ فیزیک دانشگاه شهیدبهشتی بودم). قصد دارم طی این نوشته، تجربههای خودم از دوران کارشناسی فیزیک رو بنویسم. امیدوارم این نوشته برای کسایی که قصد دارن فیزیک رو به صورت آکادمیک شروع کنن و برای کسانی که به تازگی وارد فیزیک شدن مفید واقع بشه! لطفا اگر شما هم چنین تجربهای داشتید و میتونید به این نوشته چیزی اضافه کنید حتما در قسمت نظرات بهش اشاره کنید.
-
فیزیک اون چیزی که فکر میکنید نیست: حکایت سیب و نیوتون رو فراموش کنید!

چیزی که ما توی دبیرستان به عنوان فیزیک میخونیم -صرف نظر از نوع مدرسه و معلمهایی که داشتیم – یا چیزهایی که در جامعه در مورد فیزیک یافیزیکدانها گفته میشه کلا یک سری چرند و پرنده! داستانهای علمی و قصههایی که به عنوان فیزیک توی دوران دبیرستان میخونیم با فیزیک واقعی فرق زیادی داره. به عنوان مثال، ماجرای برخورد سیب با سر نیوتون و کشف قانون گرانش عمومی رو در نظر بگیرید. احساسی که شما نسبت به این ماجرا دارید قبل و بعد از کارشناسی فیزیک متفاوته! درستی این داستان رو نمیشه انکار کرد چون توی منابع مختلفی اومده، با این وجود اینکه شما بفهمید چه عظمتی پشت این ماجرا وجود داره، نیازمند زمانی برای تامل در فیزیکه. منظورم از عظمت، فهمیدن اینه که سقوط سیب و گردش زمین به دور خورشید در حقیقت یک علت داره! این چیزی بود که نیوتون فهمید، نیوتون یک وحدت زیبا رو کشف کرد! شاید بگید: «نه، این که خیلی واضحه! هر بچه دبیرستانی اینو میفهمه!» ولی باور کنید احساسی که به این موضوع دارید و هیجانی که از درک عظمت کار نیوتون درک میکنید واقعا متفاوت خواهد بود. احساس و شهود شما به مراتب تغییر خواهد کرد و این دلیل اصلی ادعا من بر اینه که پس از تموم شدن دوره کارشناسیتون میفهمید که فیزیک اون چیزی که قبلا فکر میکردید نیست. البته به شرطی که دانشجوی خوبی بوده باشید 😉
خلاصه اینکه کمکم احساساتون نسبت به فیزیک، حین دوره کارشناسی، دچار تغییر و بهروزرسانی میشه تا اینکه پس از مدتی به این میرسید که: اگر این فیزیکه پس اونیکه قبلا بهش میگفتیم فیزیک چی بود؟! و این تبعاتی داره؛ بعضیها از این شناخت هیجانزده میشن ولی بعضیها – که تعداد این گروه از قضا بیشتره – مکافات میگیرن! تفاوت عمده از اینجا شروع میشه که توی دانشگاه ما فیزیک رو به همراه چارچوب ریاضی محکم و استواری که فیزیک برش بنا شده یاد میگیریم، به نحوی که هر گزاره یا ادعایی که مطرح میکنیم رو باید با یک عبارت دقیق ریاضی بیانش کنیم. زبان فیزیک، ریاضیاته و فیزیک بدون ریاضی، گنگ و لاله! ویدیوهای مختلف که به عنوان ویدیوهای عامهپسند (popular science) توسط بعضی از دانشمندا ساخته میشه فاقد ریاضی و پر از حرفهای هیجان انگیز و عجیبوغریب هستن. برای همینه که مردم ازشون خوششون میاد و این گمان رو میکنن که فیزیک همینه! به همین خاطر، خیلیها موقع دست و پنجه نرم کردن با ریاضیات، اون حس خوبی که نسبت به فیزیک داشتن رو از دست میدن و کمکم فیزیک براشون تبدیل به یک کابوس میشه. کابوسی که ۴ سال همراهشونه و رهاشون هم نمیکنه! البته هستند عدهای که این کار اونا رو به وجد میاره و از هماهنگی بینظیر طبیعت و ریاضیات لذت میبرن، اما کم هستن متاسفانه! (شکرخدا من از این دسته بودم). برای همین پیشنهاد میکنم اگر اهل این نیستید که زیاد ریاضی یادبگیرید و به کارببندید شاید بهتره بیخیال فیزیک بشید! متاسفانه رشته فیزیک اینجوریه که در هر لحظه ممکنه شما ازش متنفر بشید! تعارف که نداریم، سخته و زمانبر! راه میونبر هم نداره. روزی بطلمیوس یکم سوتر(حاکم وقت) از اقلیدوس پرسید: «آیا راه میونبری برای یادگیری هندسه وجود داره» و اقلیدوس جواب داد: «هیچ راه شاهانهای برای هندسه وجود نداره!» برای یادگیری فیزیک هم همینطور، هیچ راه شاهانهای وجود نداره و شما به راحتی نمیتونید یک فیزیکدان خوب بشید!
یکی دیگه از مواردی که سبب میشه دیدتون نسبت به قبل در مورد فیزیک عوض بشه اینه که با گذشت زمان، کمکم با شاخههای مختلف فیزیک آشنا میشید و کاربردهای عجیب و غریب فیزیک رو میبینید و حیرتزده میشید. اما باز هم وقتی وارد مشغول گذروندن دروس تخصص یک گرایش یا مشغول تحقیق در یک گرایش خاص میشید ممکنه حس حیرت به نفرت تبدیل بشه و یا اینکه دیگه همهچی عادی بشه ولذتی نبرید! یکی از مثالهای خوب، گرایش هستهای هست! فیزیکهستهای در ایران به خاطر شهرتی که به سبب مسائل سیاسی پیدا کرده برای خیلی از مردم جذاب به نظر میرسه، خوبه که بدونید، معمولا دانشجوهای فیزیک، بعد از گذروندن درس «فیزیک هستهای ۱ و آزمایشگاه» از علاقهشون به مقدار زیادی کاسته میشه. زمانی هم که وارد حوزه تحقیق و پژوهش میشن که دیگه واویلا! البته فیزیک هستهای به خاطر شرایط خاص سیاسی حاکم بر اون کمی با سایر گرایشها فرق داره با این وجود در سایر رشتهها هم مشکلات متعددی وجود داره. خیلی از دانشجوهایی که به نجوم علاقمند بودن و در زمان دانشآموزیشون فعالیتهای نجوم آماتوری هم انجام میدادن، کمکم در دانشگاه دچار تردیدهای زیادی در مورد ادامه تحصیل در گرایشهای نجوم، اخترفیزیک و کیهانشناسی میشن! ادلهی خیلی از این دسته هم اینه که دیگه برامون جذاب نیست، خیلی سخت یا تخصصی شده! البته باز هم عدهای هستن که هر چی میگذره بر هیجانشون افزوده میشه! این دسته کسایین که وجودشون دلگرمی به آدم میده. اینها همون کسایی هستن که امید رو در دل دانشگاه زنده نگه میدارن. مشکل این دسته در کم بودن تعدادشونه! یکی دیگه از گرایشهای فیزیک، فیزیک ماده چگال هست که صرف نظر از پایههای نظری استوار، کاربردهای وحشتناک زیبایی داره! فیزیک ماده چگال ارتباط و همپوشانی زیادی با بقیه علوم داره و نزدیکترین پل بین فیزیک و سایر رشتهها حساب میشه. این قضیه سبب میشه که بچهها کنجکاوانه و با تمایل شدیدی سراغ ماده چگال برن، اما زمانی که مشغول گذروندن درس «حالت جامد۱» و «حالت جامد۲» هستن باید قیافههاشونو ببینید! به هر حال، زیبایی و سخت بودن فیزیک همیشه به طور تنگاتنگی در زمان تحصیل یک دانشجوی فیزیک وجود داره و این خود دانشجو هست که انتخاب میکنه که کدوم رو ببینه: سختی رو یا زیبایی رو!

فیزیک نه فلسفه است و نه ریاضی! مهندسی هم که اصلا نیست! اگر به فلسفه علاقمندید و فکر میکنید که خب فیزیک و فلسفه یک چیز هستن، سخت در اشتباهید! درسته که در جاهایی تعاملاتی بین فیزیک و فلسفه وجود داره و این دو بر هم اثر میذارن، ولی این که به عنوان رشته تحصیلی فیزیک رو به جای فلسفه انتخاب کنید خیلی اذیت میشید، بهتر بگم، نه تنها خودتون اذیت میشید بلکه بقیه رو هم اذیت میکنید! همین طور اگر شدیدا به ریاضی علاقمند باشید، درسته که فیزیک نزدیکترین رشته به ریاضی هست، با این وجود به خاطر تفاوتهایی که بین نگاههای فیزیکدانها و ریاضیدانها به مسائل وجود داره باز هم ممکنه اذیت بشید! البته افرادی که به جای فلسفه یا ریاضی وارد فیزیک میشن نسبت به کسایی که به جای مهندسی وارد فیزیک میشن خیلی کمه! قسمت بد ماجرا اینه که خیلیها (مخصوصا تهرانیها و ساکنین شهرهای بزرگ ایران!) که امیدی به قبولی در رشتههای مهندسی ندارن، میگن خب فیزیک مادر مهندسیه، اشکالی نداره، فیزیک هم میزنیم! این افراد رومخترین ورودیهای دانشکده فیزیک هستن! برای اینکه خیلی زود میفهمن که فیزیک از اون «تو بمیری»ها نیست! شدیدا توصیه میکنم اگر مهندسی رو دوست دارید، مهندسی بخونید. این طرز تفکر که فیزیک خوندن توی شهر خودتون بهتر از مهندسی خوندن توی یه شهر دیگهس، به نظر من، یک طرز تفکر احمقانه است! با آینده خودتون بازی نکنید! فیزیک خیلی راحت میتونه تمام انگیزههاتون رو از بین ببره و شما رو تبدیل به یک آدم به درد نخور برای جامعه کنه. اینو جدی بگیرید!
به طور خلاصه، تجربه نشون داده کسایی که واقعا عاشق فیزیک نیستن، هر چقدر باهوش یا هر چیز دیگه باشن، اگر سراغ فیزیک بیان پیشیمون میشن!
-
خبری از بازار کار مناسب، امنیت شغلی، رفاه بالا و مازراتی نیست! فیزیک و قناعت در همتنیده هستند!

هر کسی دوست داره که بازار کار مناسب و امنیت شغلی داشته باشه، چیزی که بچههای فیزیک کمکم میفهمن ندارن! اگر فیزیک اومدین زیاد توقع شغل پردرامد رو نداشته باشین! مخصوصا فیزیک نظری! فیزیکدانها با وجود حجم کار زیادی که انجام میدن، به طور متوسط، درامد زیادی ندارن. فرصتهای شغلی فیزیک در مقایسه با سایر رشتهها خیلی کم هست. در ایران، بیرون از دانشگاه واقعا خیلی سخت میشه برای یک فیزیکپیشه شغل مناسب با تحصیلاتش پیدا کرد، اگر هم بشه، تعدادشون انگشتشماره! برای همین، یکی از سختترین قسمتهای زندگی یک فیزیک پیشه، داشتن دکتری فیزیک با جیب خالیه! در خارج از کشور باز شرایط بهتره، ولی باز هم در مقایسه با سایر رشتهها، فیزیک فرصت چندانی به شما نمیده (هرچند که اخیرا فرصتهای زیادی در موسسات مالی و شرکتهای مختلفی برای فیزیکدانها پیشاومده). شاید بهتره این جوری بگم، اگر قصدتون ثروتمند شدنه، فیزیک گزینه مناسبی نیست! شما به عنوان یک فیزیکپیشه، از علم لذت میبرید و علم براتون هیجانانگیزه، برای همین با وجود اینکه لباستون فلان مارک خاص نیست یا اینکه ماشینتون یک پرایده زیاد اذیت نمیشید، چون سرتون به جای دیگه گرمه. اما ممکنه زن و بچهتون مثل شما دیگه فکر نکنن! برای همین این یک مسئله نگرانکننده میشه اگر خونواده شما مثل خودتون نتونن قناعت پیشه کنن! البته اگر بخوام جانب انصاف رو رعایت کنم، باید بگم کسایی هم هستن که رشتهشون فیزیک بوده و الان پول خوبی به جیب میزنن! ولی یادتون باشه، من دارم یک بحث آماری میکنم، به این معنی که معمولا پزشکها یا مهندسها درآمد بیشتری نسبت به فیزیکپیشهها دارن!
-
اشتباهات دوران کارشناسی فیزیک من!
این بخش، کاملا شخصی هست، به این معنی که ممکنه مواردی که من به عنوان اشتباه طبقهبندی میکنم از نظر بعضیها اشتباه نباشه و از طرف دیگه ممکنه من طی چهار سال گذشته کارهایی انجام داده باشم که از نظر بعضیها اشتباه بوده باشه ولی من لیستش نکردم! با این وجود به نظرم حرفهایی که میزنم حرفهای معقولی هستن! به من اعتماد کنید 🙂
۱) به نظرم بزرگترین اشتباه من در دوران کارشناسی، کم مسئله حل کردن بود! حقیقتش، تا زمانی که مجبور نبودم، مسئلهای حل نمیکردم. حتما باید استاد درسی تمرینی مشخص میکرد یا اینکه شب امتحان میشد تا من دست به قلم میشدم! اما الان فهمیدم که حل مسئله باید رویه ثابت هر دانشجوی علومپایه باشه. حل مسئله باید پیوسته باشه و نه فقط در روزهای خاص (مثلا شب قبل روزی که باید تمرینهای الکترومغناطیس رو تحویل داد!). اشتباه دیگه در مورد مسئله حل کردن، گارد گرفتن در مورد نوع مسئله بود! گاهی اوقات واکنش من به بعضی از مسئلههایی که خارج از کلاس درس مطرح میشد این بود که مثلا من الان مکانیک تحلیلی خوب یادم نیست، یا الان باید فقط مسئلههای فلان درس رو حل کنم، یا اینکه الان روابط فلان چیز رو فراموش کردم، یا الان وقتش نیست! الان فهمیدم که آدم همیشه باید با گارد باز با هر مسئلهای روبهرو بشه و تا جایی که میتونه کلنجار بره. مهمترین نکته اینه که آدم بیخیال مسئله نشه! خیلی از اوقات وقتی آدم واقعا درگیر مسئله باشه، ممکنه جواب رو توی خواب پیدا کنه! این اتفاق برای من واقعا رخ داده!

۲) باید اعتراف کنم که خیلی از اوقات من شبِ امتحانی بودم! خیلی از اوقات تازه یکی دو شب قبل از امتحان ترم شروع میکردم با مبحثی آشنا شدن یا اینکه ۷ جلسه پشت سر هم، کورس دیدن! درسته که معمولا هم جواب میداد، مثلا من کوانتوم۱ رو با همین روش ۱۸/۵ شدم و کوانتوم۲ رو ۱۹/۵! با این وجود اتفاقی که افتاد این بود که من یه نمره خوب گرفتم ولی «یادگیری» واقعا حاصل نشد! کتاب درس قطعات نیمرسانا رو فقط دوبار باز کردم، شب قبل امتحان میانترم و شب قبل پایان ترم! چیزی که باید بهش اشاره کنم اینه که شما میتونید با شب امتحانی بودن هم نمره خوبی بگیرید، اما اگر صادق باشید با خودتون، چیزی یاد نگرفتید! من واقعا اینو دیگه فهمیدم که یادگیری یک فرایند مستمره و طی یک شب یادیگری حاصل نمیشه (حداقل برای ما آدمای معمولی!). به قول جان میسون: «تدریس به صورت دنبالهای از اعمال و تعاملات و دنبالهای از تصمیمات گرفته شده توسط معلم، در زمان اتفاق میافتاد. در عوض، یادگیری، به عنوان فرایند بلوغ، حتی در زمان خواب، طی زمان اتفاق میافتد.» البته، زغال خوب و دوست ناباب رو هم دست کمنگیرید! یکی از مشکلات کلاس ما، بهتره بگم ورودی ما، این بود که هیچ وقت نتونستیم با هم مسئله حل کنیم. معمولا کسی دل به کار نمیداد. متاسفانه کسی اهل مسئله حل کردن واقعا نبود 🙁 . البته من باز هم خودم رو مقصر میدونم!
۳) یکی دیگه از اشتباهات من، جدی نگرفتن کلاس درس و کلاس حل تمرین (TA) بود! درسته که بعضی از اساتید واقعا رو مخ هستن یا اینکه بعضی از TAها سواد کافی برای مسئله حل کردن و جواب دادن به سوال شما رو ندارن، ولی اینکه آدم کلا بیخیال بشه و سر کلاس نره ضرره! من فهمیدم که میگم! گاهی از اوقات هم من فقط سر کلاس مینشستم و منفعلانه هیچ کاری انجام نمیدادم، نه یادداشتی برمیداشتم و نه تلاشی برای درگیر شدن در کلاس میکردم. خیلی از اوقات هم در صورت امکان مشغول چرت زدن بودم، مخصوصا زمانی که بدون فلاسک چایی میرفتم سر کلاس. حقیقت اینه که من مجبور بودم وقتی که باید سر کلاس صرف یادگیری و آشنایی با مفاهیم میشد رو بیرون از کلاس صرف این کارها کنم، به عبارت دیگه من وقت تلف میکردم بعضی روزا فقط سر کلاس! از طرف دیگه نرفتن به کلاس حلتمرین سبب میشد که با خیلی از مسئلهها روبهرو نشم و بدتر از اون تلاشی برای حلشون نکنم!
۴) برنامه نویسی و شبیهسازی جزو لاینفک فیزیک امروزه! من اینو تا مدتها قبول نمیکردم! همهش به خودم میگفتم مهم نیست، در صورتی که الان واقعا پشیمون هستم و همیشه خودم رو ملامت میکنم که چرا زودتر یادگیری برنامهنویسی رو به صورت حرفهای شروع نکردم! به هر حال راه دررویی وجود نداره! امروز تقریبا هر گرایشی از فیزیک رو که نگاه کنید، ناگزیر از کامپیوتر استفاده میکنند!

۵) کورس فیلم سینمایی نیست! یکی از اشتباهات من این بود که فرقی بین تماشای God Father با کورس کوانتوم قائل نمیشدم! در صورتی که کورس هم مثل کلاس درسه. باید موقع دیدنش آدم یادداشت برداری کنه، بعد از تموم شدن هر قسمت، مطالعه کنه، مسئله حل کنه، یادداشتهاش رو کامل کنه و بعد از مرور اینها جلسهی بعدی کورس رو ببینه! حقیقتش من هیچ کدوم از این کارها رو تا مدتها نمیکردم. درسته که این خودش از کورس ندیدن خیلی بهتره، ولی با این وجود بازده کار رو خیلی کاهش میده و یادگیری واقعی رخ نمیده. راستش خیلی از کورسهایی که دیدم رو بعد از دو – سه سال واقعا فراموش کردم و تنها راه یادآوری دوباره دیدن اونهاست! در صورتی که اگر یادداشت برداری خوبی کرده بودم، هر موقع که نیاز داشته باشم میتونم سریع مرور کنم!
۶) یکی از مسخرهترین اشتباهات من این بود که گاهی از اوقات زوری درس میخوندم! گاهی از اوقات خسته بودم یا واقعا بیحوصله بودم ولی با این وجود سعی میکردم که به جای استراحت کردن و تجدید قوا زوری درس بخونم. درس خوندنی که یا حواسم پرت میشد وسطش یا اینکه کلی کار دیگه از جمله بیهدف چرخیدن توی اینترنت رو به همراه داشت. اشتباه من این بود که مدتها تفریح رو از زندگیم بیرون گذاشته بودم و به طور کاملا یکنواختی زندگی میکردم. زندگی نیاز داره به تنوع و استراحت. درسته که کار حرفهای نیاز به تمرین زیاد و صرف زمان زیادی داره، با این وجود گاهی از اوقات آدم باید روحیهی خودش رو تقویت کنه و به خودش استراحتی بده تا بتونه با انرژی و انگیزه سر کارش برگرده. خلاصه اینکه خیلی وقتا من فقط ادای یادگیری رو در میاوردم!

من به خاطر علاقهم اومدم فیزیک و زمانی هم که انتخاب رشته کردم، انتخابهای اولم فیزیک بود و انتخابهای دومم ریاضی. فیزیک رو دوست داشتم و همیشه با تمام مشکلات زندگی ازش لذت میبردم و میبرم. الان هم آماده تحصیلات تکمیلی هستم. من یه دانشجوی معمولی بودم، نه نخبه بودم و نه چیز دیگه. به نظرم برای فیزیک خوندن اصلیترین فاکتور علاقه است، علاقهای که ناشی از شناخت کامل باشه. همونجور که گفتم این انتخاب شخصه که بین مشاهدهی سختیهای راه و زیباییها کدوم رو انتخاب کنه. طی این پست من تجربهی خودم رو از ۴ سال فیزیک خوندن گفتم، امیدوارم این پست ایدهی خوبی بهتون از کارشناسی فیزیک بده و خودتون رو به خاطر ناآگاهی دستی دستی بدبخت نکنید. یادتون باشه، فیزیک رشته سختیه، اگر واقعا علاقمند هستید واردش بشید. هنگامی هم که واردش شدید یادتون باشه که برای چی اومدین. خودتون رو گول نزنین و با تمام قوا سعی کنید کنجکاوانه چیزهای مختلفی یادبگیرید. در هر شرایطی مسئله حل کنید و فراموش نکنید که کار یک فیزیکدان حل مسئله است! اگر هم فکر میکنید اشتباه اومدین، سریع یا تغییر رشته بدید و یا انصراف. زندگی ارزشش رو نداره که وقتتون رو صرف چیزی که کنید بهش علاقه ندارید!
در انتها به خودم واجب میدونم که از این آدمها به خاطر تمام کمکهایی که بهم طی این چهار سال کردند، تشکر کنم: شاهین شریفی، داوود معصومی، امید مومنزاده، دکتر حمیدرضا سپنجی، دکتر غلامرضا جعفری، دکتر مجید محسنی، دکتر محمدصادق موحد و دکتر علی حسینی.
راستی، اگر از من پرسیده بشه که اگر به گذشته برگردی، آیا باز هم فیزیک رو انتخاب میکنی، در جواب شعر فروغ رو خواهم گفت: «زندگی گر هزار باره بود/ بار ديگر تو بار ديگر تو»

 این پست، اشارهی مستقیمی دارد به مقاله «استفاده از ساختهای نظری برای تدریس آگاهانه»
این پست، اشارهی مستقیمی دارد به مقاله «استفاده از ساختهای نظری برای تدریس آگاهانه»





 راس ایجاد میکنه. بعد از اون، در هر مرحله، راسی اضافه میشه و به
راس ایجاد میکنه. بعد از اون، در هر مرحله، راسی اضافه میشه و به 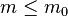 راس قبلی وصل میشه. این m راس بر اساس درجهشون انتخاب میشند: یعنی احتمال اینکه راس جدید به iامین راس موجود درگراف وصل بشه برابره با نسبت درجه راس iام به مجموع درجات کل رئوس. این سبب میشه که «هاب» در شبکه بهوجود بیاد. هابها رئوسی هستند که درجه شون از بقیه رئوس شبکه بیشتره. (صفحه شجریان در اینستاگرام یک هاب به حساب میاد در بین خوانندهها همونجوری که گوگل یک هابه در بین سایتها!). يادتون باشه که در مدل باراباشی-آلبرت وزن هر یال ۱ است!
راس قبلی وصل میشه. این m راس بر اساس درجهشون انتخاب میشند: یعنی احتمال اینکه راس جدید به iامین راس موجود درگراف وصل بشه برابره با نسبت درجه راس iام به مجموع درجات کل رئوس. این سبب میشه که «هاب» در شبکه بهوجود بیاد. هابها رئوسی هستند که درجه شون از بقیه رئوس شبکه بیشتره. (صفحه شجریان در اینستاگرام یک هاب به حساب میاد در بین خوانندهها همونجوری که گوگل یک هابه در بین سایتها!). يادتون باشه که در مدل باراباشی-آلبرت وزن هر یال ۱ است!