
(CC BY)
Using Mathematics to Study How People Influence Each Other’s Opinions
انسانها گاهی عقاید خود را در حین بحث با یکدیگر تغییر میدهند. محققان میتوانند با استفاده از ریاضیات این تغییر نظرات را در رویدادهای ساده شده زندگی روزمره بررسی کنند. این سناریوهای ساده شده که در واقع مدلهای ریاضی هستند به دانشمندان کمک میکنند تا تاثیر انسانها بر یکدیگر را از طریق ارتباطات اجتماعی بررسی کنند. در دنیای دیجیتال امروز این مدلها میتوانند به ما کمک کنند تا یاد بگیریم چگونه اطلاعات درست را ترویج و پخش کنیم و جلوی پخش اطلاعات نادرست را بگیریم. در این مقاله ما یک مدل ساده ریاضی برای تغییرات ایدهها، که برخاسته از بر همکنشهای اجتماعی است را بررسی میکنیم. ما به طور خلاصه شرح میدهیم که مدلهای تغییر نظرات چه به ما میگویند و چگونه دانشمندان سعی میکنند آنها را واقعیتر کنند.
Front. Young Minds. 12:1253153. doi: 10.3389/frym.2024.1253153
دانشمندان چگونه تغییر نظرات را بررسی میکنند؟
در داستان کوتاه «به سوی ابدیت» نوشته الیزابت بر یکی از شخصیتهای داستان میگوید: عقاید همانند بچه گربهها هستند، مردم همیشه آنها را به دیگران میبخشند، همه نظراتی دارند نظرات ما در طول زمان تغییر میکنند و اکثر مواقع نظرات ما تاثیر گرفته از نظرات دیگران هستند. بسیاری از دانشمندان تغییر عقاید در طول زمان و اثر انسانها روی آنها را بررسی میکنند. آنها اغلب از ریاضیات برای بررسی این ایدهها و پیشبینی در مورد چگونگی تغییر دیدگاهها و شکلگیری دیدگاههای مشترک مردم استفاده میکنند.
تصور کنید که مدرسه شما در حال طراحی دوباره لوگوی مدرسه و رنگ آن باشد. مدیر مدرسه اعلام کرده است که هیئت امنای مدرسه دو رنگ ممکنه یعنی آبی و قرمز را انتخاب کردهاند و دانش آموزان میتوانند با رای گیری انتخاب کنند کدام یک از این دو رنگ اصلی مدرسه باشد. در طول ناهار شما و دوستانتان به دور یک میز نشستهاید و در حال بحث در مورد رنگ جدید هستید. فرض کنید که در هر زمان تنها دو نفر از شما در حال بحث در مورد رنگ باشند. همینطور فرض کنید که شما رنگ قرمز را ترجیح میدهید. شما به سمت یکی از دوستانتان برمیگردید تا در مورد رنگ بحث کنید. دوستتان به شما میگوید که رنگ آبی روی تیشرتهای مدرسه بهتر به نظر میرسد و شما را متقاعد میکند که آبی را ترجیح دهید. بعد از آن دوست دیگری به سمت شما برمیگردد تا در مورد رنگ با شما صحبت کند و شما این دوستتان را متقاعد میکنید که او هم آبی را ترجیح دهد. تصور کنید که این صحبتهای دوتایی تا زمانی که در نهایت همه سر میز ناهار متقاعد شوند که یک رنگ را انتخاب کنند ادامه داشته باشد.
ما میتوانیم فرآیند مباحثهای که گفته شد را با یک مدل ریاضی بررسی کنیم. محققان از مدلهای ریاضی استفاده میکنند تا تغییر نظرات به خاطر برهم کنشهای اجتماعی را بررسی کنند، همانند آنچه که در صحبتهای میز غذا رخ داد. محققان اغلب مدلهای ساده را که به راحتی قابل فهم هستند را بررسی میکنند. یکی از مدلهایی که محققان برای بررسی آنچه مثل شرایطی که در بالا گفته شد استفاده میکنند مدل «رای دهنده» نام دارد که برخلاف نامش هیچ ربطی به رای دادن ندارد. مدلهای رای دهنده دو جز کلیدی دارند اول: نظر ابتدایی مردم یعنی چیزی که مردم قبل از بحث کردن با دیگران فکر میکنند و دوم یک قانون به روز رسانی: که چگونگی تغییر عقاید مردم را توصیف میکند. در مثال ما عقاید اولیه رنگهای آبی و قرمزی هستند که دانشآموزان در ابتدا ترجیح میدهند. برای قانون به روز رسانی در مدل رای دهنده ما به طور تصادفی دو نفر را انتخاب میکنیم و سپس به طور تصادفی عقیده یکی از آنها را برای جمعشان بعد از بحث انتخاب میکنیم. هر کدام از دو عقیده به طور برابر محتمل هستند. فرض کنید برای انتخاب یکی از عقاید به طور تصادفی یک سکه پرتاب میکنیم. اگر دو نفر قبل از بحث عقیده یکسانی داشته باشند همچنان میتوانیم آنها را انتخاب کنیم که با یکدیگر در مورد عقیدهشان صحبت کنند. با این حال در این مورد عقیدهشان یکسان باقی میماند. این قانون به روز رسانی بحثی را که در آن یک نفر میتواند عقیده دیگری را در مورد رنگ مورد علاقهاش تغییر دهد شبیهسازی میکند. این قانون به روز رسانی ساده جزئیات زیادی در مورد کنش روزمره انسانها با یکدیگر به ما نمیدهد. به طور مثال این قانون به روز رسانی شامل هیچ خاطرهای از بحثهای گذشته نیست. با این حال با وجود ماهیت ساده لوحانه این قانون همچنان به محققان برای بررسی تغییرات عقاید در طول زمان کمک میکند.
در شکل اول ارتباط مدل رای دهنده با مثال ما از دوستانی که در مورد رنگهای مورد علاقهشان در هنگام ناهار بحث میکنند را میبینیم. وقتی همه با هم در مورد رنگ توافق میکنند به اجماع میرسند. وقتی انسانها به اجماع نمیرسند ما میگوییم که آنها نظرات پراکنده دارند به این معنا که بیش از دو نظر متفاوت وجود دارد. در مدل رای دهنده محققان علاقمندند که بدانند آیا در نهایت مردم به اجماع میرسند یا نه و اگر به اجماع میرسند چه مدت زمانی طول میکشد تا به آن برسند.
در ابتدا (در زمان t = 0)، هر حیوان آبی یا قرمز را برای رنگ اصلی مدرسه ترجیح می دهد. در زمان t = 1، پرنده و گربه در مورد رنگ مدرسه بحث می کنند و تصمیم می گیرند که آبی را ترجیح دهند. در زمان t = 2، گربه و خوک در مورد رنگ مدرسه بحث می کنند. آنها یک رنگ را ترجیح می دهند، بنابراین نظرات آنها تغییر نمی کند. در زمان t = 3، سگ و گوسفند در مورد رنگ مدرسه بحث می کنند و تصمیم می گیرند که قرمز را ترجیح می دهند. به روز رسانی نظرات تا زمانی که حیوانات به اجماع برسند ادامه می یابد. در این مثال، در زمان t = 20، همه آبی را ترجیح می دهند.
ادغام شبکههای اجتماعی در مدلهای عقیده
در مثال رنگ مدرسهای که زدیم گروه کوچکی از دوستان در مورد رنگ ترجیحیشان دو به دو بحث میکنند. فرض کنید که این بحثها در مدرسه بزرگی که همه دانش آموزان یکدیگر را نمیشناسند رخ میدهند. محققان میتوانند مجموعه روابط اجتماعی داخل مدرسه را با شبکه اجتماعی از دانش آموزان نشان دهند. دانش آموزان راسهای این شبکه اجتماعی هستند و روابط اجتماعی که دانش آموزان را به هم متصل میکنند را با یالها نشان میدهیم. اگر دو نفر با هم رابطه اجتماعی داشته باشند در اصطلاح به آنها همسایه در شبکه میگوییم. در مثال ما اگر دو راس با هم دوست باشند بین آنها یال وجود دارد. وقتی محققان یک مدل رای دهنده را روی یک شبکه اجتماعی بررسی میکنند تنها راسهای همسایه میتوانند روی عقیده یکدیگر تاثیر بگذارند. یعنی آنها فرض میکنند که فقط افراد دارای یک رابطه اجتماعی میتوانند مستقیماً روی یکدیگر تاثیر بگذارند. به عنوان مثال دانش آموزان یک مدرسه تمایل دارند روی دوستان خود تاثیر بگذارد. استفاده از شبکههای اجتماعی به محققان امکان مطالعه تاثیر ساختار شبکه( یعنی چه کسی با چه کسی دوست است) بر روی تغییر عقاید را میدهد.
یک شبکه اجتماعی دوستی بین دانش آموزان یک مدرسه را در نظر بگیرید. اجازه دهید مدل رای دهنده را روی این شبکه اجتماعی بررسی کنیم. همانند قبل هر دانش آموز در ابتدا قرمز یا آبی را ترجیح میدهد با این حال برخلاف مثال اولیه ما که بدون شبکه اجتماعی بود برخی افراد با یکدیگر دوست نیستند. دو نفر تنها در صورتی با یکدیگر در مورد ترجیحات خود صحبت میکنند که با هم دوست باشند در هر به روز رسانی مدل ما به طور تصادفی یک جفت دوست را برای صحبت با یکدیگر انتخاب میکنیم. یعنی در شبکه اجتماعی دانش آموزان همسایگان را انتخاب میکنیم. سپس به طور تصادفی یکی از نظرات آنها را انتخاب میکنیم و فرض میکنیم که هر دو دانش آموز پس از بحث با این نظر موافق باشند. همانند قبل این به روز رسانی نشان دهنده آن است که یک نفر دوست خود را متقاعد میکند که همان رنگی را ترجیح دهد که او ترجیح میدهد. در شکل دو نمونهای از نحوه به روز رسانی مدل رای دهنده را در یک شبکه اجتماعی بسیار کوچک مشاهده میکنید. نظرات با گذشت زمان تغییر میکنند و در نهایت هر دانشآموز موافقت میکند که به همان یک رنگ رای دهد. یعنی دانش آموزان در نهایت به اجماع میرسند. متاسفانه در زندگی واقعی ممکن است زمان زیادی طول بکشد تا به یک اجماع برسیم. یک مدرسه ممکن است برای تصمیم گیری در مورد رنگ انقدر صبر نکند. برای بررسی موقعیتهای از این دست محققان بررسی میکنند که چگونه نظرات در یک مدل رای دهنده در طول زمان مشخصی مانند یک هفته تغییر میکنند تا ببینند که آیا اجماع حاصل میشود یا خیر. محققین همچنین بررسی میکنند که چه مدت زمانی طول میکشد تا یک اجماع در شبکه ظهور کند.

افراد (راسها) دایره های توپر و دوستیها (یالها) خطوط سیاهی است که راسها را به هم متصل می کند. راسها را با نظر آنها (آبی یا قرمز) رنگ می کنیم. در زمان t = 0، ما شبکه اجتماعی و نظرات اولیه همه را نشان می دهیم. برخلاف شکل ۱، فقط دوستان (یعنی راسهای همسایه) می توانند تعامل داشته باشند. برخی از مردم با یکدیگر دوست هستند، اما برخی دیگر دوست نیستند. در هر زمان، ما به صورت تصادفی دو دوست را برای تعامل و به روز رسانی نظرات آنها انتخاب میکنیم.
هنگام مطالعه یک مدل رای دهنده یک انتخاب ممکن آن است که به طور تصادفی نظرات اولیه گروه را تعیین کنیم با این حال در مثال ما ترجیحات اولیه رنگ احتمالاً از یک فرایند تصادفی مانند پرتاب سکه ناشی نمیشوند. بسیاری از مردم رنگ خاصی را ترجیح میدهند و رنگهای دیگر را دوست ندارد. این ترجیحات ممکن است به دلایل زیادی ایجاد شود. شاید کسی اغلب یک لباس آبی میپوشد و یا شاید تیم مورد علاقهای به رنگ آبی دارد. همچنین ممکن است فردی بخواهد از رنگی که با رنگ تیم ورزشی رقیب همخوانی دارد اجتناب کند در یک شبکه اجتماعی مدرسه جوامعی از افراد با دوستیهای زیادی در داخل جامعه وجود دارد. به عنوان مثال جوامع دوستی میتوانند از کلاسها باشگاههای مدرسه یا تیمهای ورزشی ایجاد شوند. احتمال دوستی افرادی که در یک جمع مشخص قرار دارند بیشتر از احتمال دوستی افراد از جمع های مختلف است. همانطور که در شکل سوم مشاهده میکنید محققان میتوانند نظرات اولیه را بر اساس چنین جوامعی انتخاب کنند. به طور مثال فرض کنید رنگ تیم فوتبال محلی آبی است. شاید دانش آموزان کلاس هفتم بیشتر از دانش آموزان کلاس هشتم طرفدار این تیم باشند بنابراین شاید دانش آموزان کلاس هفتم بیشتر از کلاس هشتم آبی را به عنوان رنگ اصلی مدرسه ترجیح دهند. محققان بررسی میکنند که چگونه جوامع شبکههای اجتماعی بر نتایج مدلهای رای دهنده و به طور کلیتر چگونه بر نظرات مردم تاثیر میگذارند.
یک شبکه اجتماعی با دو جامعه – دانش آموزان کلاس هفتم و کلاس هشتم – را در نظر بگیرید که به ترتیب آبی و قرمز را ترجیح می دهند. (الف) در زمان t = 0، ما انتخاب می کنیم که هر دانش آموز کدام رنگ را ترجیح می دهد. با استفاده از همین اولویتهای اولیه، مدل رأیدهنده را بارها در کامپیوتر شبیهسازی میکنیم. (ب) در یک شبیه سازی، دانش آموزان در نهایت رنگ آبی را ترجیح می دهند. (ث) در شبیه سازی دیگری، دانش آموزان در نهایت رنگ قرمز را ترجیح می دهند. (د) در شبیهسازی دیگر، دو جامعه هنوز ترجیحات متفاوتی در زمان t = 15 دارند. ما این شبیهسازی را تا زمانی ادامه میدهیم که همه دانشآموزان به یک اجماع برسند.
مدلهای عقیده اغلب شامل تصادفی بودن هستند. در مدل رای دهنده این تصادفی بودن در انتخاب نظرات اولیه، تعیین اینکه کدام جفت از افراد برای مکالمه با یکدیگر انتخاب شوند و تعیین اینکه نظر کدام یک از دو نفر به عنوان نظر جمعشان انتخاب میشود ظاهر میشود. در شکل سه میبینید که تصادفی بودن میتواند باعث شود که از یک مدل ریاضی نتایج کاملا متفاوتی حاصل شود. محققان باید هنگام تعیین اینکه آیا تفاوت در نتایج مدل ناشی از ویژگیهای شبکه اجتماعی است مانند جوامع داخل شبکه یا از تصادفی بودن حاصل شده است دقت به خرج دهند. آنها اغلب از شبیه سازیهای کامپیوتری برای مطالعه مدلهای عقیده استفاده میکنند و مهم است که یک مدل مانند مدل رای دهنده را بارها شبیه سازی کنیم تا نتایج احتمالی آن را به دقت بررسی کنیم.
از مدل رای دهنده چه میتوانیم بیاموزیم؟
چرا محققان به مدلهای رای دهنده و سایر مدلهای نظری علاقمند هستند؟ تصمیم گیری در مورد رنگ جدید مدرسه ممکن است چندان مهم به نظر نرسد با این حال مطالعه مدلهای عقیده میتواند به محققان کمک کند تا تغییرات در افکار عمومی در مورد موضوعات مهمی مانند انتخابات ریاست جمهوری و سیاستهای واکسیناسیون را بررسی کنند. مدلهای عقیده میتوانند بینشهایی در مورد چگونگی اشاعه اطلاعات دقیق و اینکه چگونه استفاده از رسانههای اجتماعی میتواند بر دیدگاههای ما تاثیر بگذارد ارائه دهد. رسانههای اجتماعی نحوه تعامل مردم و نحوه انتشار نظرات را تغییر دادهاند. به طور مثال رسانههای اجتماعی بر دیدگاه مردم در مورد کووید ۱۹ تاثیر گذاشتند. رسانههای اجتماعی میتوانند به مقامات بهداشتی کمک کنند تا راهنماییهای مهمی مانند اطلاعات در مورد واکسنها را به اشتراک بگذارند. از طرف دیگر متاسفانه رسانههای اجتماعی میتوانند به انتشار اطلاعات نادرست و گمراه کننده کمک کنند که میتواند به سلامت روحی و جسمی بسیاری از افراد آسیب برساند.
محققان در بسیاری از موضوعات از جمله ریاضیات، روانشناسی، جامعه شناسی، زیست شناسی، فیزیک، اقتصاد، علوم کامپیوتر و غیره به دلایل مختلف مدلهای عقیده را مطالعه میکنند. ریاضیدانان و فیزیکدانان اغلب این مدلها را به دلیل جالب بودن مطالعه میکنند. دانشمندان علوم سیاسی از مدلهای عقیده برای مطالعه قطبی شدن نتایج رای گیری در انتخابات استفاده میکنند. در تجارت مدلهای عقیده برای مطالعه تصمیمهای قیمت گذاری در بازارهای مالی، بررسی محصول در فروش آنلاین و اثرات کمپینهای تبلیغاتی مورد استفاده قرار گرفتهاند. محققان همچنین چگونگی اثر متقابل تغییر عقاید و پخش بیماریها را با مدلهای ترکیبی بررسی کردهاند.
مدلهای رای دهنده کاربردهای زیادی دارند و ما میتوانیم با واقع بینانهتر کردن آنها بهره بیشتری از آنها ببریم. چگونه میتوانیم مدلهای رای دهنده را واقع بینانهتر کنیم؟ در یک مدل رای دهنده ما به طور تصادفی تعیین میکنیم که پس از تعامل دو نفر کدام نظر را به عنوان نظر مشترکشان انتخاب کنند. با این حال در واقعیت دقیقاً مشخص نیست که مردم چگونه نظرات خود را شکل میدهند و چگونه آنها را تغییر میدهند. همچنین نظرات مردم با فاکتورهای دیگری به غیر از تاثیر مستقیم افراد شکل میگیرند. تشکیل و تغییر عقاید فرایند پیچیدهای است بنابراین مدل سازی ریاضی در مورد آن دشوار است. قانون به روز رسانی مدل رای دهنده واقعیت را بیش از حد ساده میکند بنابراین محققان سعی کردهاند که این به روز رسانی را به واقعیت نزدیکتر کنند. همچنین محققان انواع دیگری از مدلهای عقیده را توسعه دادهاند مانند مدلهایی که شامل افراد سرسختی میشوند که بعید است نظرات خود را تغییر دهند، تا ایدههای مختلفی را در مورد چگونگی تغییر نظرات افراد در خود بگنجانند. آنها همچنین مدلهای عقیدهای را توسعه دادهاند که مفاهیمی همچون فشار همگروهیان را در بر میگیرد. به عنوان مثال شاید برخی از افراد فقط نظر خود را به نظری تغییر دهند که به اندازه کافی در بین دوستانشان محبوب باشد مثلاً زمانی که حداقل ۵ نفر از دوستانشان این نظر را داشته باشند. محققان همچنین مدلهای عقیدهای را بررسی میکنند که در آنها ساختار شبکهی اجتماعی و تغییر نظرات به یکدیگر وابسته هستند . به عنوان مثال اگر شما با کسی در مورد موضوع مهمی تفاوت شدید عقیده دارید ممکن است او را در اینستاگرام یا تیک تاک دنبال نکنید.
خلاصه و از اینجا به کجا میرویم؟
مطالعه اینکه چگونه تعاملات اجتماعی بین افراد بر نظرات آنها تاثیر میگذارد روشی جذاب برای استفاده از ریاضیات است. محققان مدلهای نظری جدیدی را برای توسعه بینش در مورد تعاملات انسانی و تاثیرات آن بر پدیدههای اجتماعی ایجاد میکنند. این مدلها بسیار سادهتر از تغییر عقاید در واقعیت هستند. چالش اصلی در مدل سازی عقاید ارزیابی مدلها از طریق مقایسه آنها با نظرات موجود در دادههای دنیای واقعی است. محققان فعالانه در تلاشند تا راههای مناسبی برای انجام این کار پیدا کنند. با این حال و با وجود چالشها مدلهای عقیده همچنان به محققان کمک میکنند تا بیاموزند که چگونه تعاملات اجتماعی بر نظرات ما تاثیر میگذارند. همانگونه که محققان مدلهای عقاید بیشتری را توسعه میدهند ما در مورد چگونگی تغییر عقاید و تاثیر این تغییرات بر رفتار انسان بیشتر میآموزیم.
برای دیدن منابع و جزئیات بیشتر به اصل نوشته حتما نگاه کنید.


 در پست قبل
در پست قبل

 راس ایجاد میکنه. بعد از اون، در هر مرحله، راسی اضافه میشه و به
راس ایجاد میکنه. بعد از اون، در هر مرحله، راسی اضافه میشه و به 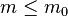 راس قبلی وصل میشه. این m راس بر اساس درجهشون انتخاب میشند: یعنی احتمال اینکه راس جدید به iامین راس موجود درگراف وصل بشه برابره با نسبت درجه راس iام به مجموع درجات کل رئوس. این سبب میشه که «هاب» در شبکه بهوجود بیاد. هابها رئوسی هستند که درجه شون از بقیه رئوس شبکه بیشتره. (صفحه شجریان در اینستاگرام یک هاب به حساب میاد در بین خوانندهها همونجوری که گوگل یک هابه در بین سایتها!). يادتون باشه که در مدل باراباشی-آلبرت وزن هر یال ۱ است!
راس قبلی وصل میشه. این m راس بر اساس درجهشون انتخاب میشند: یعنی احتمال اینکه راس جدید به iامین راس موجود درگراف وصل بشه برابره با نسبت درجه راس iام به مجموع درجات کل رئوس. این سبب میشه که «هاب» در شبکه بهوجود بیاد. هابها رئوسی هستند که درجه شون از بقیه رئوس شبکه بیشتره. (صفحه شجریان در اینستاگرام یک هاب به حساب میاد در بین خوانندهها همونجوری که گوگل یک هابه در بین سایتها!). يادتون باشه که در مدل باراباشی-آلبرت وزن هر یال ۱ است!






