برچسب: صفحه مختلط

توی قسمت قبلی دیدیم که اگر هر تابع f رو داشته باشیم می‌تونیم برای اون تابع مجموعه‌ی ژولیای مربوط به اون رو پیدا کنیم که خب یکمی از کامپیوتر هم کمک گرفتیم. کار ما این بود که یک تابع رو بر می‌داشتیم شرایط اولیه‌ای (یک سری نقطه توی فضای مختلطی (موهومی)) بهش می‌دادیم، مقدار تابع رو به ازای اون شرایط اولیه به دست می‌اوردیم و همین طور دوباره این مقدار رو به تابع می‌دادیم و این روند رو ادامه میدادیم تا ببینیم آیا شرایط اولیه‌ای که انتخاب کردیم به بی‌نهایت میل میکنه یا نه، اگر نمی‌کرد اون موقع مجموعه‌ی ژولیا اون تابع رو تشکیل میداد.  همین طور گفتیم که از بین همه‌ی توابع، توابعی که به صورت چندجمله‌ای های مربعی می‌باشند بیشتر مشهور هستند؛ توابعی با فورم: $$f(z)=z^2 +c$$توی این پست در مورد علت این شهرت توضیح میدم؛

تابع ${f(z)=z^2 +c}$ رو در نظر بگیرید؛ فراموش نکنید که c می‌تونه هر عددی – ولی حتما مختلط – باشه. حالا اگر با نقطه‌ی z=0 شروع کنیم، به این دنباله‌ می‌رسیم:

  $$  c , c² + c , (c²+c)² + c , ((c²+c)²+c)² + c , (((c²+c)²+c)²+c)² + c , …$$

اگر این دنباله واگرا نباشه، یعنی اگر c هایی انتخاب کنیم که در نهایت این دنباله به بی‌نهایت نرسه اون موقع مجموعه‌ی ژولیایی که توسط این cها برای تابع  ${f(z)=z^2 +c}$ ساخته میشه، «همبند» هست. احتمالای توی نظریه‌ی گراف با مفهموم همبند بودن آشنا شدین (معمولا سال آخر دبیرستان بچه‌های رشته‌ی ریاضی فیزیک نظریه‌ی گراف رو توی درس ریاضیات گسسته می‌خونند!) اگر نشدین، همبند بودن یک جور مفهموم متصل بودن رو داره، وقتی یک گراف یا شبکه‌ای همبند باشه اونموقع اگر شما از یک نقطه‌ای شروع به حرکت کردید، می‌تونید به هر نقطه‌ای که دلتون می‌خواد برید وبدون اینکه جایی مسیرتون قطع بشه. خلاصه این که اگر دنباله‌ای که ساختیم واگرا

نشد اون موقع ما یک مجموعه‌ی ژولیای همبند می‌تونیم بسازیم. (اثبات این مطلب فراتر از حوصله‌ی ماست!) خب حالا این مجموعه‌ی ژولیای همبند به چه دردی می‌خوره آیا؟! اجازه بدید تا یک مجموعه‌ی جدید معرفی کنیم به نام «مجموعه‌ی مندلبرو».

«مجموعه مندلبرو شامل نقاطی (c) از صفحه‌ی مختلط هست که به ازای آن ها مجموعه‌ی ژولیا تابع ${f(z)=z^2 +c}$ همبند باشد.»

شما می‌تونید یک برنامه بنویسید تا براتون مقادیری که C ممکنه بگیره رو پیدا کنه ولی یک نکته‌ای هست و اون اینه که همه‌ی مجموعه‌های ژولیا همبند شامل نقطه‌ی 0 = 0+ z= 0i  هستند! بنابراین «اربیت» یا «چرخش» یا «تکرار» مبدا برای این دسته از مجموعه ها، همیشه باید یک مقدار کران‌دار باشه و به بی‌نهایت میل نکنه، پس نقطه‌ی صفر در همه‌ی مجموعه‌های ژولیای همبند صدق میکنه. به طور مشابه در همه‌ی مجموعه‌های ژولیای ناهمبند نقطه‌ی صفر وجود نداره! خب این یک سنگ محکی شد برای تشخیص اینکه آیا نقطه c دلخواهی عضو مجموعه‌ی مندلبرو هست یا نه! یعنی کافیه تا ما «اربیت» یا «چرخش» یا «تکرار» نقطه‌ی z=0 رو برای تابع  ${f(z)=z^2 +c}$ بررسی کنیم، اگر مقادیری که به دست میاند (همون «اربیت» یا «چرخش») کران‌دار باشند اون موقع اون c مورد نظر ما عضو مجموعه مندلبرو هست ولی اگر به بی‌نهایت میل کنه اون‌موقع اون c دیگه عضو مجموعه مندلبرو نیست! شرمنده 😀

مجموعه‌ی مندلبرو یکی از موضوعات دینامیک مختلطه که برای اولین بار ایده‌ش اوایل قرن بیستم توسط ریاضی‌دانان فرانسوی بهنام «فاتو» و«ژولیا» مطرح شد. اون موقع‌ها هنوز کامپیوتر زیاد رونق نداشت برای همین مثلا فاتو نتونست شهود و تصویر خوبی از این مجموعه ارائه بده. تا اینکه مندلبرو اول مارس ۱۹۸۰(اواخر قرن بیستم!) به لطف کامپیوترهای شرکت IBM تونست این کار رو انجام بده و بعدش هم این موضوع رو گسترش زیادی داد. آدم‌های زیادی بعد از مندلبرو روی این موضوع کار کردند ولی به خاطر خدمات مندلبرو یا به احترام مندلبرو، اسم این مجوعه رو «مجموعه مندلبرو» گذاشتند!

این مجموعه در حقیقت یک فرکتال هست با مرز بسیار بسیار پیچیده، جوری که شیشیکورا ثابت کرد (۱۹۹۸) که بعد این مرز ۲ هست! این فرکتال برخلاف مجموعه‌ی ژولیا کاملا خودمتشابه نیست و اگر روی شکل زوم کنید این رو به راحتی متوجه خواهید شد!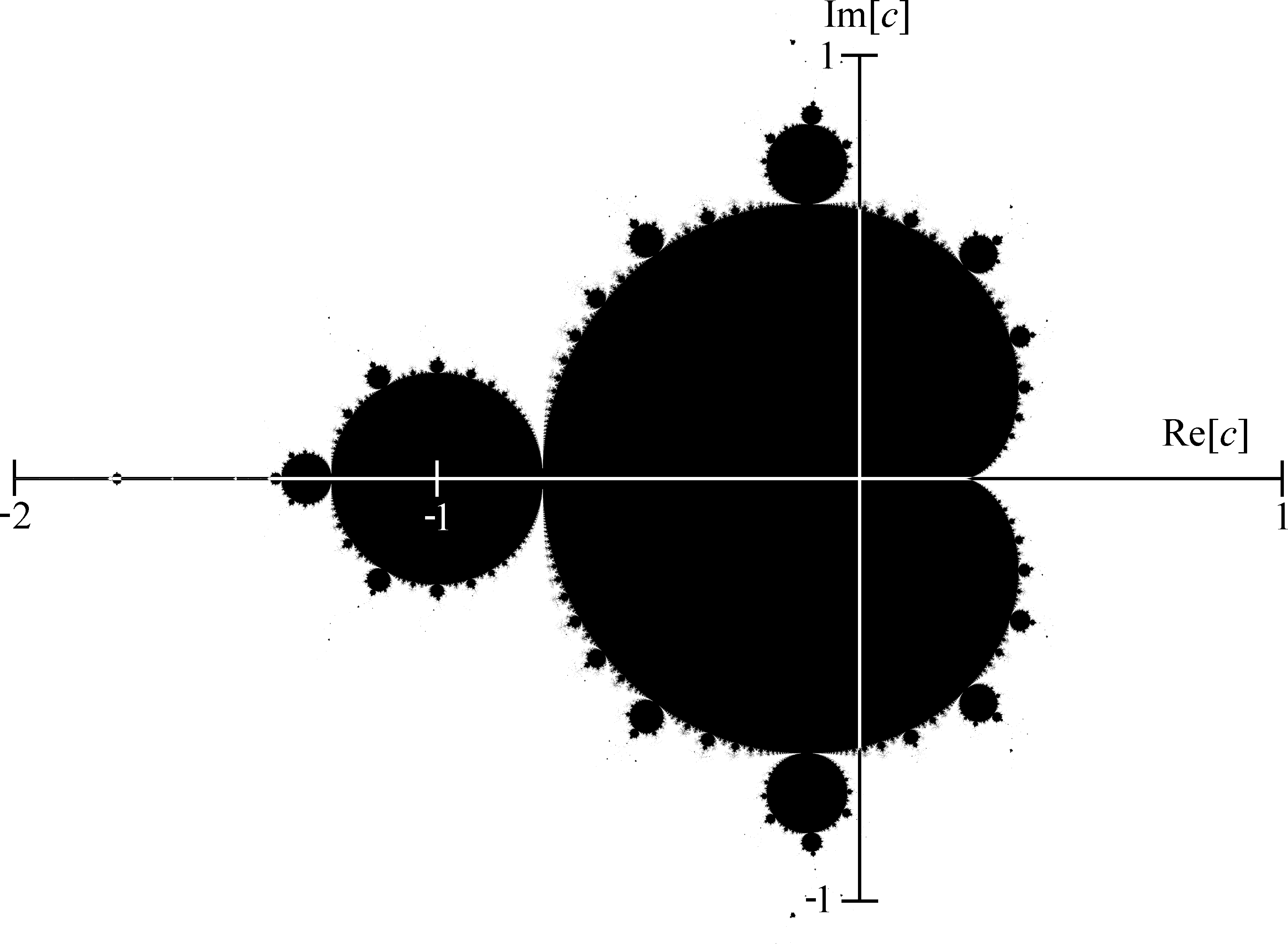

همین طور این مجموعه توی صفحه‌ی مختلط، توی دیسکی یه شعاع ۲ قرار میگیره و  تقاطع اون با محور حقیقی بازه [۰/۲۵, ۲-] هست. حدودا دو سال پیش مساحت مجموعه مندلبرو 0.0000000028 ± 1.5065918849 واحدمربع تخمین زده شد! پیشنهاد می‌کنم حتما به صفحه‌ی ویکی پدیای این مجوعه عجیب و غریب  سر بزنید، مخصوصا اگر دوست دارید که الگوریتم‌هایی که برای تولید این دسته از فرکتال‌ها مورد استفاده قرار می‌گیرند چه جوری هستند!

برای مطالعه، پیشنهاد میکنم کتاب زیر رو بخونید، خیلی خوب توضیح داده هم فرکتال‌ها رو هم آشوب رو!

David P. Feldman, Chaos and Fractals, An Elementary Introduction, Oxford University

به عنوان حسن ختام، یک جمله از مندلبرو رو نقل میکنم (از سخنرانی تد ۲۰۱۰) : «خب، اجازه دهید تمام کنم. این شکل در اینجا تنها از یک تمرین در ریاضیات محض بوجود آمد. ظهور شگفتی های بی پایان از قواعد ساده، که بی نهایت تکرار می شوند.»