چرا رياضى ياد مىگيريم؟ اساسا، بخاطر سه دليله: محاسبه، كاربرد، و آخرى، و متاسفانه كمترين از لحاظ زمانى كه به اون اختصاص مىديم، الهام بخش بودنه! رياضى علم الگوهاست، و اون رو مطالعه مىكنيم تا ياد بگيريم چطور منطقى، منتقدانه و خلاقانه فكر كنيم، اما بخش خيلى زيادى از رياضى كه تو مدرسه ياد مىگيريم بطور موثرى انگیزه دهنده نيست، و وقتى هم میپرسیم، “چرا اين را ياد مىگيريم؟” چيزى كه اغلب مىشنویم اينه كه به زودی میفهمید! یا فوقش اگه دانشجوی فیزیک هم باشید، موقع تدریس درس «ریاضی فیزیک» میگند این توی فلان جای کوانتوم کاربرد داره! خب این اصلا خوب نیست! بهترنیست هر از گاهى رياضى رو فقط به خاطر این انجام بدیم که جالبه يا زيباست؟ يا به اين خاطر كه ذهن را به هيجان مياره؟ بذارید براتون مثالی بزنم از دنباله اعداد دلخواهم، اعداد فيبوناچى!
$$ 1 1 2 3 5 8 … $$
$$ a_1=1 $$ $$ a_2=1 $$ $$ a_{n+1}= a_n +a_{n-1} $$
از نقطه نظر محاسبه، فهمیدنشون آسونه! مثلا یک بعلاوه یک که میشه دو. بعد یک بعلاوه دو که میشه سه، دو بعلاوه سه پنج میشه، سه بعلاوه پنج هم هشت، و الی آخر. از لحاظ کاربرد، اعداد فیبوناچی اغلب در طبیعت بطرزی شگفت آور ظاهر میشند. تعداد گلبرگهای یک گل عموما عددی فیبوناچی است، یا تعداد مارپیچهای روی یک گل آفتابگردان یا يك آناناس همینطور از قاعده سری فیبوناچی پیروی میکنند.
در حقیقت، کابردهای خیلی بیشتری دربرگیرنده ارقام فیبوناچی میشه، اما چیزی که بیش ازهمه دربارشون میفهمیم الگوهای عددی زیبایی هستند. فرض کنیم شما از محاسبه مربع کامل اعداد خوشتون میاد:
$$ 1 1 2 3 5 8 13 … $$
$$ 1 1 4 9 25 64 169 … $$
به این مربعهای کامل از چند تا عدد اول فيبوناچى نگاه كنيم. شما وقتى مربعهاى كامل را با هم جمع مىكنيد انتظار نداريد چيز خاصى اتفاق بيفته. اما اين را ببينيد:
$$ 1+1=2 $$
$$ 1+4=5 $$
$$ 4+9=13 $$
$$ … $$
$$ a_{n-1}^2 + a_n^2 = a_{n+1} $$
در واقع، يكى ديگه هم هست. فرض كنيد كه ميخواستيد مربعهاى كامل چند تا عدد فيبوناچى اول را جمع كنيد. بذارييد ببينيم به كجا ميرسيم:
$$ 1+1+4=6 $$
$$ 1+1+4+9=15 $$
$$ 1+1+4+9+4+25=40 $$
$$ 1+1+4+9+25+64=104 $$
$$ … $$
حالا به اون اعداد نگاه كنيد. اونها اعداد فيبوناچى نيستند، ولی اگه با دقت بهشون نگاه كنيد، خواهيد ديد كه اعداد فيبوناچى درون اونها مخفى شدند! تونستید اونا رو ببینید:
$$ 6=2*3 $$
$$ 15=3*5 $$
$$ 40=5*8 $$
$$ 104=8*13 $$
$$ … $$
ولی چرا:
$$ 1+1+4+9+25+64 = 1^2 + 1^2 + 2^2 + 3^2 + 5^2 + 8^2 =104 $$
بذارید یه کار جالب انجام بدیم! با یک مربع یک در یک شروع میکنیم و بعدش یک مربع یک در یک دیگه رو میذاربم. با هم دیگه، اونها یک مستطیل یک در دویی را تشکیل میدند. زیر اون، یه مربع دو در دویی رو قرار میدیم، و بغل اون، یک مربع سه در سه، دوباره زیر اون، یک مربع پنج در پنج. و بعديك مربع هشت در هشت! الان يك مستطيل بزرگ ساختیم، اينطور نيست؟
حالا بذارييد یه سوال ساده بپرسیم: مساحت مستطيل چقدره؟ خب، از يك طرف، جمع مساحتهاى مربعهاى داخل اونه، اينطور نيست؟ درست همانطور كه اون رو خلق كرديم. یک مربع كامل بعلاوه یک مربع كامل بعلاوه مربع كامل دو بعلاوه مربع كامل سه بعلاوه مربع كامل پنج بعلاوه مربع كامل هشت. اینطور نیست؟ از طرف ديگه، مساحت اون برابر حاصلضرب طولش درعرض اونه.
پس:
$$ S = 1^2 + 1^2 + 2^2 + 3^2 + 5^2 + 8^2 =104 $$
$$ S = 8 * (5+8) = 8 * 13 $$
که ۱۳ عدد بعد از ۸ توی دنباله فیبوناچی هست!
الان اگر به اين فرايند ادامه بديم، مستطيلهاىی با اعداد ٢١ در ١٣، ۲۱ در ۳۴ توليد خواهيم كرد و الى آخر.
خب الان اين را امتحان كنيد. اگر ١٣ را تقسيم بر ٨ كنيد، به ١/٦٢٥ مىرسيد.
$$ 13/ 8 = 1.625 $$
$$ 21/13 = 1.615 $$
$$ 34/21 = 1.619 $$
$$ 55/34 = 1.6176 $$
$$ 89/55 = 1.61818 $$
و اگر عدد بزرگتر را به عدد كوچكتر تقسيم كنيم، اين ضريب

ها به رقمى در حدود ١/٦١٨ نزديك و نزديكتر مىشود، كه از سوى خيلىها بعنوان ضريب طلايى شناخته مىشود،رقمى كه رياضيدانها، دانشمندان و هنرمندان را قرنهاست كه مجذوب كرده. شاید بزودی یه چیزی هم در مورد نسبت طلایی بنویسم!
برای مثال اگه یک مربع a در a رو کنار یک مستطیل a در b بذاریم (a>b) اون موقع یک مستطیل a در a+b داریم! نسبت طول این مستطیل به عرضش، همون نسب طلاییه!
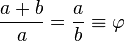
یاد آوری کنم که جواب عدد زیر عدد طلاییه:

![]()
ما زمان زيادى را صرف يادگيرى درباره محاسبه كردن مىكنيم، اما بياييد كاربرد رو هم فراموش نكنيم، از جمله، شايد، مهمترين كاربرد از همه آنها، ياد بگيريم چطور فكر كنيم.
ویکی پدیا یه منبع قابل اعتماده! همین طور پیشنهاد میکنم این ویدیو رو ببینید چون که یکی از منابع هست :
