سرطان به عنوان یکی از بیماری‌های که این روزها نامش بر سرزبان‌ها افتاده است، نامی است که به مجموعه‌ای از بیماری‌هایی اطلاق میشود که از تکثیر مهارنشده سلول‌ها پدید می‌آیند. سرطان عموما به عنوان بیماری ژن‌ها شناخته میشود؛ به این معنا که تغییرات ژنتیکی می‌توانند منجر به بروز این عارضه شود. از سوی دیگر، تلاش‌های صورت گرفته پیرامون کنترل و درمان سرطان عمدتا بر اساس شناخت ژن‌های موثر در سرطان‌های مختلف، تاکنون با چالش‌های زیادی همراه بوده است. در نگاه پیچیدگی، حرکت‌های جمعی برآمده از برهمکنش‌های یک سیستم بس‌ذره‌ای (سلول) تنها با مطالعه اجزای آن سیستم (ژن‌ها) قابل توصیف نیست و با دانستن اینکه هر جز (ژن) چگونه کار می‌کند، نمی‌توان درک کاملی از مقیاسی بزرگ‌تر (سلول) با سازمان‌دهی مرتبه-بالاتری پیدا کرد. در مورد ژن‌ها می‌دانیم که بیان هر ژن بر بیان سایر ژن‌ها اثر می‌گذارد و وجود این همبستگی‌ها سبب تشکیل یک حرکت جمعی میشود که خود باعث اثر گذاشتن روی بیان سایر ژن‌ها میشود. هدف این مطالعه، نگاهی پدیدارشناسانه به سرطان سینه و مقایسه رفتار جمعی ژن‌ها در نمونه سالم و سرطانی است. با در نظر گرفتن سلول به عنوان یک سیستم پیچیده، می‌خواهیم شبکه پیچیده‌ای که در پس این سیستم نشسته است را مورد مطالعه قرار دهیم به امید این که درک بهتری از سرطان از نگاه پیچیدگی پیدا کنیم.
بدین منظور، با در نظر گرفتن هر ژن به عنوان یک اسپین و برهمکنش ژن با ژن به عنوان ضریب جفت‌شدگی بین دو اسپین متناظر با آن‌ها در یک مدل شیشه-اسپینی (مدل گاوسی چند متغیره)، به دنبال استنباط این ضرایب هستیم. برای این کار با استفاده از اصل بیشینه آنتروپی، ماتریس برهمکنش را برای نمونه سالم و سرطانی یافته و از روی آن شبکه تنظیم ژن را برای دو نمونه بازسازی می‌کنیم. این شبکه‌ها، دارای یال‌هایی با وزن‌های مثبت و منفی هستند، بنابراین می‌توانیم در چارچوب نظریه توازن به این شبکه‌ها انرژی نسبت دهیم و تمایل شبکه‌ها نسبت به تغییر وضعیتشان را مورد بررسی قرار دهیم. نتایج ما نشان می‌دهد که توزیع مثلث‌های ایجاد شده در شبکه از یک الگوی توانی پیروی می‌کند. از نقطه نظر چشم‌انداز انرژی، انرژی شبکه سالم از شبکه سرطانی بیشتر است و این به معنای پویایی بیشتر سلول سالم نسبت به سرطانی است. شبکه سرطانی تمایل کم‌تری نسبت به تغییر وضعیت خود دارد و به همین خاطر دسترسی کم‌تری به وضعیت‌های قابل دسترس خود پیدا می‌کند. از سوی دیگر، در شبکه سرطانی، تعداد یال بیشتری دیده میشود. وجود یال بیشتر، به معنای ارتباط بیشتر بین اجزا و تاثیر بر دینامیک سلول است. رهیافت دنبال‌شده در این مطالعه به ما در یافتن درک بهتری از سلول به عنوان یک سیستم پیچیده کمک می‌کند.
| ارجاع به اثر: | arXiv:2010.05897 [q-bio.MN] |
2010.05897
به همت دبیرستان علامه حلی۱ تهران، کارسوق (کارگاه) پیچیدگی‌های طبیعت رو برگزار کردم.
در پست قبل
راس ایجاد می‌کنه. بعد از اون، در هر مرحله، راسی اضافه میشه و به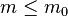 
راس قبلی وصل میشه. این m راس بر اساس درجه‌شون انتخاب میشند: یعنی احتمال اینکه راس جدید به iامین راس موجود درگراف وصل بشه برابره با نسبت درجه راس iام به مجموع درجات کل رئوس. این سبب میشه که «هاب» در شبکه به‌وجود بیاد. هاب‌ها رئوسی هستند که درجه شون از بقیه رئوس شبکه بیشتره. (صفحه شجریان در اینستاگرام یک هاب به حساب میاد در بین خواننده‌ها همون‌جوری که گوگل یک هابه در بین سایت‌ها!). يادتون باشه که در مدل باراباشی-آلبرت وزن هر یال ۱ است!