برچسب: نسبیت

ویراستار: متن پیش رو نخستین بار توسط این نویسنده در سی‌ و سومین‌ شماره‌ی تکانه (نشریه علمی-آموزشی دانشجویان فیزیک دانشگاه صنعتی شریف) آمده. نویسنده از آقای علی گودرزی، آقای دکتر سامان مقیمی، آقای حسین مهدئی و آقای امیرحسین پیله‌وریان و همچنین خانم حانیه ملکی تشکر می‌کند.

برای درک بهتر این نوشته، سیتپور شنیدن این پادکست را پیشنهاد می‌کند:

---

فروکاست‌گرایی

فروکاست‌گرایی یا تقلیل‌گرایی باوری فلسفی است که همه‌ی قوانین حاکم بر طبیعت را می‌توان با تعداد کمی از «قوانین بنیادی» توصیف کرد. به‌عنوان مثال، این باور احتمالا رایج که رفتار یک سامانه دارای تعداد زیادی «ذره» (به‌عنوان مثال جعبه‌ای شامل تعداد زیادی مولکول گاز یا رفتارهای موجودی زنده که از تعداد زیادی مولکول تشکیل شده‌ است) را می توان از طریق برآیند رفتار تک‌تک ذرات توصیف کرد، که البته حقیقت بدیهی‌ای به نظر نمی‌آید، از این باور فلسفی نشأت می‌گیرد. مثلا بیوفیزیک‌دانان در مقیاس «بنیادی‌تری» نسبت به زیست‌شناسان کار می‌کنند و تلاش می‌کنند برخی رفتارهای موجودات زنده را از طریق فیزیک حاکم بر مولکول‌ها و مواردی از این قبیل توصیف کنند. در این مقاله به طور خاص به فروکاست‌گرایی در فیزیک و بخشی از تأثیر آن در روند پیشرفت علم فیزیک می‌پردازیم.

 از نظر تاریخی احتمالا این باور از حدود زمان گالیله و نیوتن به طور جدی‌تر وارد فیزیک شده ‌است. شاید معروف‌ترین شاهد آن تلاش نیوتن برای نوشتن قانون گرانش باشد؛ او سعی کرد به قانونی برسد که  تمام برهمکنش‌های گرانشی را توضیح دهد. تلاش او در این راستا بود که حرکت سیارات، سقوط اجسام بر روی زمین و مواردی از این دست را بتواند با یک قانون واحد توضیح دهد. یک نکته‌ی قابل بحث این است که به نظر نمی‌آید الزامی برای «وجود» قانونی واحد باشد که همه‌ی برهمکنش‌های گرانشی را توضیح دهد.  به نظر می‌آید از نظر تاریخی، در ادامه و بعد از زمان گالیله و نیوتن‌ این نگرش به مرور بیشتر وارد فیزیک شده ‌است. چند الگوی جالب و مشخص‌تر در برخی اتفاقات پررنگ‌ مربوط به این دیدگاه در علم فیزیک مشاهده می‌شود که به آن‌ها خواهیم پرداخت (هر چند که این دسته‌بندی شامل همه الگوها نمی‌شود و لزوما یکتا نیست).

نظریه موثر

زیاد پیش می‌آید که در فیزیک، نظریه‌ی توجیه کننده‌ای پدیده‌ای — که با مشاهدات تعارض خاصی ندارد — را به عنوان نظریه‌ی موثر یک نظریه‌ی بنیادی‌تر بنویسند. یکی از معروف‌ترین تلاش‌ها در این راستا ساختن مکانیک آماری است، که کل نظریه‌ی ترمودینامیک را به مکانیک بس ذره‌ای تقلیل می‌هد و تلاش می‌کند با روش‌های آماری، ترمودینامیک را به عنوان نظریه‌ی موثری از مکانیک نیوتنی و بعد از آن مکانیک کوانتومی بسازد. هر گاه بین نظریه‌ی به نسبت پذیرفته شده موجود و مشاهدات (تجربه) تعارضاتی مشاهده شود، فیزیکدان‌ها تلاش می‌کنند تا با رعایت اصل هم‌خوانی، نظریه‌ی جدیدی بسازند؛ به این معنا که نظریه‌ی جدید باید در حالات حدی مشخصی نتایج نظریه‌ی سابق را مجنر شود. مثلا نظریه‌ی نسبیت یا مکانیک کوانتومی که در پی هم‌خوان نبودن مشاهدات تجربی با نظریه‌های کلاسیک ساخته شدند در حدهایی نتایج مکانیک کلاسیک را بازتولید می‌کند. به هر حال، نظریه‌ مکانیک کلاسیک کامل نیست ولی در برخی حدود بسیار خوب کار می‌کند. به قول فاینمن، علم در مورد این نیست که چه چیز درست یا نادرست است، بلکه در مورد این است که ما چه چیز را با چه دقتی می‌توانیم توصیف کنیم. مکانیک کلاسیک برای سرعت‌های پایین یا اندازه‌های خاصی در اکثر موارد با دقت خوبی با مشاهدات ما هم‌خوانی دارند. نظریه‌های پیشرفته‌تری چون مکانیک کوانتومی و نسبیت هم در این حدود تبدیل می‌شوند به مکانیک کلاسیک. گاهی نظریه‌های جدید برای از بین بردن تعارضات دو نظریه جا افتاده تهیه می‌شوند. مثلا سوای مشاهدات آزمایش مایکلسون – مورلی، نسبیت خاص به دنبال بهبود نظریه مکانیک کلاسیک برای هم‌خوانی با نتایج نظریه الکترومغناطیس ساخته شد.

پدیدارگی

گاهی در سامانه‌های بس‌ذره‌ای ویژگی‌های جدیدی اصطلاحا«پدیدار می‌شوند» بی‌آن‌که ذرات سازنده آن سامانه آن ویژگی یا ویژگی‌ها را در خود داشته باشند. از طرف دیگر، رفتار برخی سامانه‌ها در سطوح مختلف را بدون دانستن سطوح بالاتر یا پایین‌تر آن می‌توان فهمید. پدیدارگی یا پدیدار شدگی به به‌وجود آمدن ویژگی‌های یک سامانه در سطوح بالاتر پیچیدگی اشاره دارد که در تک تک اجزای آن در سطح پیچیدگی کمتر قابل مشاهده نیست و فقط در برآیند کل سامانه و با در نظر گرفتن کل اجزا و برهمکنش‌هایشان می‌توان آن‌ها را دید. فیلیپ اندرسون در مقاله‌‌ای با عنوان «بیشتر، متفاوت است» این ایده را مطرح کرد که برای درک برخی از پدیده‌ها، پرداختن به نظریه‌های «بنیادی‌تر» لزوما سودمندتر نیست. مثلا انتظار می رود که علی‌الاصول کل شیمی را از فیزیک بس‌ذره‌ای بتوان را استخراج کرد. اندرسون این ایده را مطرح می‌کند که این نظریه‌های موثر که در سطوح پیچیدگی بالاتری ساخته می‌شوند باید (از نظر خودش) به همان اندازه «بنیادی» تلقی شوند که نظریه‌های با سطح پیچیدگی کمتر تلقی می‌شوند، چون عملا بسیاری از اوقات «بنیادی‌ترین» چیزی هستند که با آن می‌توان مشاهدات را توصیف کرد. اندرسون از این دیدگاه  انتقاد می‌کند که گاهی تنها به فیزیکدانان ذرات بنیادی به عنوان کسانی که کار «بنیادی» می‌کنند نگاه می‌شود، اما نظریه‌های ذرات بنیادی در عمل نمی‌توانند بسیاری از پدیده‌هایی که مشاهده می‌کنیم و حاصل برهمکنش تعداد زیادی ذره هستند را توصیف کنند. 

یکی دیگر از موارد قابل ذکر این است که نظریه‌های در سطوح پیچیدگی بالاتر خیلی اوقات برگرفته و حاصل تقریباتی از نظریه‌های بنیادی‌تر هستند و کاملا بدون اتکا به آن‌ها نیستند. در واقع برای ساده‌تر شدن مدل و معادلات خیلی از این نوع نظریه‌ها تقریباتی را وارد می‌کنند و با در نظر گرفتن اصل نظریه بنیادی‌تر، از بسیاری از پیچیدگی‌ها صرف نظر می‌کنند. به عنوان مثال می‌توان به مدل هابارد در فیزیک ماده چگال اشاره کرد. در این مدل از برهمکنش الکترون‌های غیر نزدیک صرف نظر می‌شود و مقدار پتانسیل حاصل از برهمکنش الکترون‌های نزدیک هم به عنوان تابعی از بقیه‌ی پارامترها وارد مدل نمی‌شود. در این مورد مثلا ایده‌ی تقریب را می‌توان در قانون کولن دید، به دلیل رابطه‌ی عکس پتانسیل با فاصله، از پتانسیل ناشی از الکترون‌های در فواصل دور از هم صرف‌نظر می‌شود. در سامانه‌های پیچیده هم از این جنس ایده‌ها استفاده می‌شود. فایده‌ی این کار این است که با اجتناب از درگیر محاسبات گاهی طولانی شدن، می‌توان راحت‌تر به استنتاج نتایج حاصل از مدل پرداخت. البته میزان کارا بودن مدل ساده‌سازی شده باید با نتایج آزمایش‌ها مطابقت داده شود.   

نکته‌ی دیگری که وجود دارد بحث سودمند بودن یا نبودن توصیف پدیده‌های پیچیده توسط نظریه‌های با سطح پیچیدگی کمتر است. فرض کنید بتوان با کامپیوترهای آینده سامانه‌های بس‌ذره‌ای را با نظریه‌های در سطح اتم‌ها حل عددی کرد. مشکلی که وجود دارد این است که حجم اطلاعات به دست آمده به این صورت بسیار زیاد است و بسیاری از آن‌ها را نمی‌توان به طور مستقیم در پدیده‌هایی که نیاز به توصیفشان را داریم مشاهده کرد. مثلا یک ظرف گاز را در نظر بگیرید. حتی اگر معادلات حرکت حاکم بر تک تک ذرات را بتوانیم به صورت کلاسیک حل کنیم، مشکل بعدی این هست که چیزی که مشاهده می‌کنیم مکان تک تک ذرات نیست. تابعیت زمان مکان تک تک ذرات برای توصیف یک سامانه ترمودینامیکی کارایی خاصی ندارد. حتی در این حالت هم باید دنبال کمیت‌های موثری بگردیم، کمیت‌هایی که در این سطح از پیچیدگی پدیدار می‌شوند و سعی کنیم از حل عددی معادلات حرکت همه‌ی ذرات به طریقی به آن‌ها برسیم. در ترمودینامیک کمیت‌هایی مثل فشار و دما از این جنس هستند. 

یکی ازمشکلاتی که گاهی از نظر عملی به تلاش برای توصیف یک سامانه با تعداد کمی پارامتر توسط نظریه‌های در سطح پیچیدگی بالاتر وارد می‌شود، این است که این کار بسیار ساده‌انگاری دارد و همیشه نمی‌توان کل سامانه بس‌ذره‌ای را توسط تعداد کمی کمیت موثر توصیف کرد. دکتر خرمی در مقاله‌ای که در زمینه‌ی فروکاست‌گرایی نوشته‌اند اینطور استدلال می‌کنند که این نکته نسبتا بدیهی‌ است. می‌توان تعداد کمیت‌های موثر را بیشتر کرد (و حتی مثلا تمام ذرات گاز را در نظر گرفت) ولی به این قیمت که میزان محاسبات بیشتر شود. وقتی محدودیت توان و انرژی داشته باشیم، این نهایت کاری است که می‌توانیم بکنیم. اگر در آینده این محدودیت‌ها کمتر شد، و البته نیاز به دقت بیشتری وجود داشت، می‌توان محاسبات را دقیق‌تر کرد و آن‌ها را با نظریه‌های با سطح پیچیدگی کمتری پیش برد. مثالی که در مقاله‌شان به آن اشاره می‌کنند در مورد هواشناسی است. اینکه در گذشته به دلیل کم‌قدرت‌تر بودن کامپیوترها مجبور بودند محاسبات را ساده‌تر کنند به این قیمت که دقت پیشبینی‌ها کم می‌شد و همچنین مقیاس زمانی‌ای که پیشبینی‌ها تا آن تا حد معقولی کار می‌کردند کمتر می‌شد. ولی این نهایت کاری بود که می‌توانستند بکنند و اصطلاحا «از هیچ چیز بهتر بود». اما بعدا با قدرتمندتر شدن کامپیوترها و ابزارهای محاسبه پیشبینی‌ها بهتر شدند و تا مقیاس زمانی بزرگ‌تری قابل اتکا بودند.

در قسمت پیشین به تعریف فضا در مدل ولفرم پرداختیم و تکه آخر را که «زمان» باشد به این قسمت سپردیم. پازلی که پس از کامل شدن آن می‌توانیم به مدل‌سازی نسبیت خاص در «فضا-زمان» برسیم.

جالب این جاست که مفهوم «زمان» در مدل ولفرم از دل یک «زیر قالی نکردن» پدیدار می شود. شاید این زیر قالی مأمن امنی برای تمام مسائلی باشد که ترجیح می‌دهیم به آن‌ها فکر نکنیم. زیرا در رسیدن به مقصودمان مانع ایجاد می‌کنند اما این بار توجه ولفرم به یکی از آن‌ها باعث شده است تا مفهوم زمان را از دل آن بیرون بکشد.

«ظهور مسئله» – نقطه‌ای که علم از آن شروع می‌شود

شاید همه‌ی ما در محیط آموزشی خودمان، شبیه‌سازی نرم‌افزاری کرده‌ایم اما در حین این شبیه‌سازی با مساله‌ای مواجه شده‌ایم که آن را دانسته فرض کرده‌ایم و یا خیلی راحت از کنار آن گذشته‌ایم. به گزاره و قانون پیشین یاد شده در قسمت قبل دوباره توجه کنید. قانون تحول سامانه به این شرح است که دو یال را انتخاب و حذف می‌کنیم و یک مجموعه یال جدید جایگزین آن می‌کنیم. اما کدام دو یال؟! در مجموعه حاضر انتخاب‌های زیادی داریم و با انتخاب و تحول آن در مرحله بعد به یک گراف متمایز می‌رسیم. پس کدام دو یال را باید انتخاب کنیم؟

به شکل آشنای زیر دقت کنید در ابتدا با همان شرط اولیه و قانون یاد شده در قسمت پیشین شروع می‌کنیم اما با انتخاب جفت یال متفاوت مسیر تحول ما تغییر می‌کند. درخت زیر نشان می‌دهد که اگر در هر مرحله جفت یال متفاوتی را انتخاب کنیم چگونه گراف حاصل از دیگر مسیرها متفاوت می‌شوند.

در چنین مواردی معمولا از این جزییات چشم پوشی می‌کنیم و بدون اثبات برای خود توجیه می سازیم که در بلند مدت این تفاوت‌ها اهمیت پیدا نمی‌کنند اما چگونه و چرا این فرض را در شبیه‌سازی می‌کنیم. بی‌تردید پاسخ به آن دشوار است و ما تلاش می‌کنیم جزییاتی که نتیجه‌گیری دل‌خواهمان را به خطر می‌اندازند نبینیم!

شاید یکی از دلایل توجه نکردن به جزییات ظریف ما ریشه در «عجله‌‌ برای نتیجه» داشته باشد. در دنیای آکادمیک امروز بسیار نتیجه‌گرا شده‌ایم. زیر بار فشار تمرین و مقاله که در مدت محدود باید تمام شوند؛ خیلی از این جزییات ظریف له می شوند. این بار کسی به این جزییات دقت کرده‌است که سال‌هاست با دنیای آکادمیک صنعتی خداحافظی کرده است. یعنی ولفرم!

سخن نویسنده

«تلاش برای حل مسئله» – ذکاوت پژوهشگر

بیایید کمی این مسئله را بسط دهیم. ما یک شرایط اولیه داریم که به کمک یک قانون آن را متحول می‌کنیم. برای سادگی بیایید از تحول یک سامانه باهم حرف بزنیم که از حروف تشکیل شده است. با حالت BBBAA شروع می‌شود و قانون تحول آن به گونه زیر است.

شرط اولیه: BBBAA قانون تحول: $ { BA \rightarrow AB } $

همان طور که می‌بینید مسیرهای متفاوتی را می‌توانیم برای تحول آن بپیماییم. سوال مهم اینجاست که اگر زمان را در مدل خود همگام با گام‌های متحول سازی سامانه در نظر بگیریم دیگر خط زمانی واحدی نخواهیم داشت و در تعریف زمان دچار مشکل می‌شویم. اگر چه تمایل زیادی داریم تا «زمان» را معادل سلسله تحولات درون شبیه‌سازی خود بگیریم اما مشکل بوجود آمده نقد بزرگی به این معادلسازی وارد می‌کند.

اما زیرکی که ولفرم به خرج می‌دهد تا از پس این مشکل برآید ستودنی است. به مربع‌های زرد رنگ درون شکل توجه کنید. این مربع‌ها «رخدادهایی» را توصیف می‌کنند که طی آن حالت سامانه از یک مربع آبی به مربع آبی دیگر تغییر می‌کند. این رخداد‌ها دارای خاصیت ترتیب هستند به این معنی که نوبت هر رخداد تنها زمانی فرا می‌رسد که رخداد قبلی آن اتفاق افتاده باشد. همچنین هر رخداد زمینه ساز رخدادهای بعد خود است. این ترتیب را با نام رابطه «علت و معلولی» می‌شناسیم. حال اگر هر علت را به معلول‌های مستقیم آن متصل کنیم می‌توانیم یک گراف جدید با نام «گراف روابط علّی» بسازیم.

حال نشان می‌دهیم که چگونه گراف جدید می‌تواند مشکل بوجود آمده در توافق نداشتن خطوط زمانی بر سر تحول یکپارچه سامانه را حل و از میان بردارد. به شکل بالا مجددا دقت کنید. این درخت ۵ مسیر متفاوت را برای سیر تحول یک سامانه که با حالت مثالی BBBAA شروع می‌شود؛ توصیف می‌کند. اگر هر پنج مسیر را به صورت مجزا دنبال کنید و رخدادهای زرد رنگ و روابط آن را یادداشت کنید به پنج شکل زیر می‌رسید. هر کدام از این اشکال رخدادهای لازم برای تحول در یکی از این پنج مسیر را شرح می‌دهند.

اگر به مجموعه پنج‌تایی بالا دقت کنیم؛ متوجه نکته ظریفی می‌شویم. هر پنج گراف جهت‌دار با هم «یکریخت» هستند. اگر چه برچسب‌های هر نقطه‌ی آنها باهم فرق دارد اما هر پنج‌تا یک نقطه دارند که دو یال خروجی و یک یال ورودی دارد که از سرچشمه‌ای نشئت گرفته می‌شود که خود دو یال خروجی داده است. این به این معنی است که اگر چه مسیر‌های متفاوتی را می‌توان برای تحول این سامانه به صورت محاسباتی پیمود اما همه‌ی آنها گراف علّی مشابه دارند.

به عبارت دیگر گراف علّی ما تحت مسیرهای متفاوت تحول «ناوردا» است. در واقع این خاصیت ناوردایی حاصل از نوع قانونی است که ما برای تحول انتخاب کرده ایم. قوانینی که این ناوردایی را در گراف علّی باعث می‌شوند، قوانین «casual invariance» یا «ناوردای عِلّی» می‌دانیم. این نوع از قانون، اختلاف بین تمام مسیرهای ممکن بین تحول گراف را به توافق می‌رساند و ما را در تعریف کردن مفهوم «زمان» یاری می‌کند.

حال که کلیدواژگان #رخداد، #علت‌ومعلول و #ناوردایی را باهم دیدیم. کلیدواژه #نسبیت کم‌کم در ذهن ما به درستی تداعی می‌شود. جایی که دقیقا می‌خواهیم با زبان این مدل محاسباتی وارد آن شویم.

«نسبیت خاص» – یک اتفاق خوش!

بیاید با یک مثال ساده شروع کنیم. فرض کنید مانند قبل قرار است با یک قانون ساده، سامانه خود را متحول کنیم. یک رشته کاملا نامرتب مانند زیر درنظر بگیرید که قرار است آن را مرتب کنیم. قانون تحول آن هم به این گونه $BA \rightarrow AB$ است. این یک رشته کاملا بهم ریخته است به همین دلیل رخدادها در تک‌تک نقاط آن اتفاق می‌افتند. استفاده از این مثال به ما این امکان را می‌دهد تا رخدادها را در تمام نقاط «فضا» ببینیم.

شرط اولیه: BABABABABABABABABABA قانون تحول: $ { BA \rightarrow AB } $

فرض ‌کنید می‌خواهید قصه‌ی تحول این سامانه را برای یک شنونده روایت کنید. تا زمانی که شما ترتیب رخدادها را رعایت کرده باشید؛ بی‌تردید او به قصه‌ی شما گوش خواهد کرد و اعتراض نخواهد کرد . به این معنی که اگر ابتدا یک معلول را روایت کنید و سپس علت آن را؛ او گیج خواهد شد و روابط علّی را گم خواهد کرد.

یک روایت مثالی می‌تواند چنین باشد که از بالای گراف روابط علّی شروع می‌کنیم و به سمت پایین به ترتیب حرکت می‌کنیم. هر تعداد رخداد که می‌توانیم با رعایت ترتیب علت و معلول برای او همزمان بخوانیم را روایت کنیم. در شکل زیر، هر خط قرمز به ما نشان می‌دهد که در هر مرحله کدام رخدادها را برای شنونده بخوانیم.

حال فرض کنید که شنونده‌ی دیگری داشته باشید که با سرعت ثابت حرکت کند. حرکت او باعث می‌شود تا قصه‌ای را که تعریف می‌کنید متفاوت از شنونده اول بشنود. هر چه رخدادی در فاصله ی دورتری از او باشد با تاخیر بیشتری به دست او خواهد رسید. همین نکته باعث می شود رخدادهایی را که پیش از این شنونده‌ی اول هم‌زمان دریافت می‌کرد، دیگر همزمان دریافت نکند. در واقع خطوط «هم‌زمانی» مشابه شکل تغییر کرده است.

حرکت با سرعت ثابت نسبی است یا ما به دور جهان می‌گردیم یا جهان به دور ما!

در شکل بالا خطوط همزمانی را برای شنونده دوم رسم کردیم. اما شنونده‌ی دوم می‌تواند این طور فکر کند که این جهان است که به زیر پای او کشیده است و خودش ساکن بوده. او خود را شنونده‌ای مانند شنونده‌ی اول فرض می‌کند. پس می‌توانیم از او بخواهیم که برای ما داستانی را که شنیده است برایمان مجددا تعریف کند!

حال بیاید روایت او را از قصه‌ای که شنیده است بازسازی کنیم. برای این کار نیاز به یک تبدیل هندسی داریم. تبدیل هندسی‌ای که تمام فضای موجود در شکل بالا را به گونه‌ای تبدیل کند که خطوط مورب همزمانی شنونده دوم به حالت افقی درآیند. همچنین ترتیب روابط علی در گراف ما حفظ شود. آن تبدیل با دو شرط یاد شده، به صورت یکتا به قرار زیر درمی‌آید:

$ (t, x) \rightarrow (\frac{t – \beta x}{\sqrt{1-\beta^2}}, \frac{x – \beta t}{\sqrt{1-\beta^2}}) $

تبدیل یاد شده را با نام تبدیلات لورنتس می‌شناسیم. این تبدیلات به ما کمک می‌کنند تا دو روایت دو شنونده در حال حرکت را به یکدیگر تبدیل کنیم. همان طور که در شکل ۸ می‌بینیم شنونده‌ی دوم رخدادهای سمت چپ رشته حروف را زودتر از سمت راست می‌شنود. زیرا شنونده در حال حرکت است و خبر رخدادهای سمت راست زمان بیشتری را برای رسیدن به شنونده نیاز دارند.

حال که روایت شنونده‌ی دوم را بازسازی کردیم می‌توانیم گراف علّی بدست آمده در شکل ۸ را روی صفحه‌ی رخدادها بنشانیم و به ترتیب بخوانیم که شنونده‌ی دوم چگونه تحول سامانه را شنیده‌است.شکل ۹

همان طور که می‌بینید اگر چه شنیدن رخدادها کمی دیر و زود شده است اما هر دو شنونده در نهایت یک تغییر را برای رشته خواهند شنید. رشته حروف برای هر دو به حالت …AAABBB… خواهد رسید. این نتیجه می‌تواند با یکی از اصول نسبیت خاص انشتین معادل سازی شود. او در یکی از اصول خود ناوردایی «فیزیک» را در چارچوب‌های ناظرهای مختلف اشاره کرده بود.

همچنین قابل توجه است که می‌توانیم «اتساع زمانی» را توسط این مدل توضیح دهیم. دو رخداد از دو ردیف متوالی از شکل ۷ را در نظر بگیرید. در روایت دوم در شکل ۸ فاصله‌ی دو ردیف کمی کش آماده است. به این معنی که شنونده‌ی دوم فاصله‌ی زمانی بین آن دو رخداد را طولانی‌تر رصد می‌کند.

به این ترتیب به کمک مدل ولفرم توانستیم یکبار دیگر نسبیت خاص ونتایج آن را از نو بدست آوریم. قابل تقدیر است که این مدل در ادامه فراتر می‌رود و حتی به دنیای گرانش و کوانتوم مکانیک نیز پا می‌گذارد. برای مطالعه بیشتر در مورد این مدل می‌توانید به صفحه‌ی پروژه‌ی فیزیک ولفرم پا بگذارید. او یک کتاب الکترونیکی مصوّر را برای شرح تمامی جنبه‌های مدل خود نوشته است.

در پایان با ذکر نکته‌ای کوتاه به این دو قسمت پایان می‌دهم. شاید در حین نوشتن این مقاله بسیار به نام ولفرم اشاره کردم و تصور می‌کنم که ناخودآگاه از او بتی را وصف کرده‌ام. اما باید اینجا اشاره کنم که ولفرم نام یک گروه است و تمام این پژوهش‌ها برآمده از یک تلاش گروهی بوده است کاری که امروزه در محیط دانشگاهی خودمان کمتر به آن پرداخته‌ایم.

به تازگی کامنتی دریافت کردم که چندتا سوال ازم پرسیده بود. در این نوشته می‌خوام به این پرسش‌ها جواب بدم!

۱) زمان بر نیروی وزن اثر داره ؟ منظورم اینه وقتی زمان رو ثابت یکنیم یعنی اینکه تمام قوانین فیزیک رو با استفاده از زمان ثابت کنیم باز هم جسمی مثل لیوان به زمین برخورد میکنه اونم بر اثر نیروی گرانش یا نه؟(مثلا اگر تندی زمان رو زیاد کنیم جسمی مثل لیوان با تندی زیاد به زمین میرسه)
۲) چرا بعضی از پدیده ها در حال حرکت هستند؟ (مثل نور که وقتی لامپ رو روشن میکنیم بدون اینکه کاری بکنیم پرتوی نور خود به خود حرکت میکنه)
۳) آیا واقعا نور به دام سیاهچاله میفته ؟تا جایی که من میدونم انسان برای دیدن پدیده ها و اجسام ها به نور نیاز داره پس اگه نور از سیاهچله نمیتونه فرار کنه چطور دیدیمش؟(منظورم
عکسی که از سیاهچاله توی سال ۹۸ پارسال گرفتن)
۴) آیا نور تنها پدیده ایی هستش که سرعتی بسیار زیاد داره یا نه ؟
۵) نور ثابته ؟

۱) رابطه نیرو و زمان

قوانین نیوتون به ما میگه که اگه جسمی در حال حرکت باشه، تا زمانی که به اون جسم در کل نیرویی وارد نشه، جسم به حرکت خودش ادامه میده. اگر هم جسم از اول در حال حرکت نباشه، قاعدتا همون‌جایی که هست می‌مونه. مثل توپی که یه گوشه افتاده و تا زمانی که کسی بهش لگ نزنه از جاش تکون نمی‌خوره. منظور از «حرکت» هم تغییر موقعیت جسم با گذشت زمانه. یعنی هر بار که عقربه ساعت روی دست من تیک بزنه جسم از جایی به جای دیگه بره.

در فیزیک نیوتونی اختیار تند و کند کردن گذر زمان دست ما نیست. یعنی ما نمی‌تونیم کاری کنیم که زمان سریع‌تر بگذره یا کندتر بگذره یا اینکه متوقف بشه! ولی می‌تونیم این ایده رو شبیه‌سازی کنیم. مثل زمانی که از چیزی فیلم گرفته باشیم و با سرعت‌های مختلف اونو پخش کنیم. می‌تونیم تندتند بزنیم جلو ببینم آخرش چی میشه یا اصلا متوقفش کنیم. برای همین، اگه بتونیم که زمان رو متوقف کنیم، اون موقع اتفاقی که می‌افته اینه که آخرین تصویری که از هر چیزی داریم، همون باقی می‌مونه. پس اگه سیبی در حال سقوط به زمینه، با متوقف کردن زمان بین زمین و آسمون می‌مونه. این به این معنی نیست که نیرویی وجود نداره! بلکه به این معنی هست که در یک لحظه خاص، ما فقط یک فریم از یک فیلم رو انتخاب کردیم و داریم اونو می‌بینیم و با راه انداختن دوباره زمان، می‌بینیم که سیب به سقوطش ادامه میده. یا اگه فرض کنیم که گذر زمان رو سریع‌تر کنیم اون موقع می‌بینیم که سیب زودتر به زمین می‌خوره. یا اگه زمان رو به عقب برگردونیم می‌بینم که سیب به جای زمین خوردن، هوا میره 🙂

توضیح‌ فنی‌تر:

اگر دینامیک توصیف‌کننده یک سیستم، توسط معادلات تعینی داده بشه،اون موقع خروجی مسئله، یک «مسیر» می‌تونه باشه. مسیر، یک «خم» در فضای مکانه که توسط زمان نشانه‌گذاری شده. با داشتن مسیر، می‌تونیم بدونیم که سرشت نهایی سیستم چیه. به عنوان مثال با حل مسئله گرانش عمومی نیوتون برای دو جسم، به یک مسیر بسته بیضی شکل برای یکی از اون دو جسم می‌رسیم. با تغییر زمان، از نقطه‌ای به نقطه‌ی دیگه‌ از اون مدار (مسیر بسته) هدایت میشیم.

قانون دوم نیوتون، $F=ma$ یا معادله اویلر-لاگرانژ $\frac{\partial L(x,\dot{x}; t)}{\partial x } = \frac{d}{dt}\frac{\partial L(x,\dot{x}; t)}{\partial \dot{x} }$ هر دو منجر به دسته‌ای از معادلات دیفرانسیل معروف به معادلات حرکت میشن. در این روش مدل‌سازی، حرکت سیستم شما تعینی هست و شما با دونستن اطلاعات در مورد حال، دقیقا می‌تونید بگید که چه اتفاقی در آینده می‌افته.

گاهی دینامیک توصیف کننده شما توسط معادلات غیر تعینی داده میشه، مثل زمانی که حرکت یک ولگرد (قدم زن تصادفی) یا یک فرایند تصادفی رو مدل می‌کنید. اون موقع برای شروع مسئله، با معادله «مادر» یا معادله فوکر-پلانک می‌تونید پیش‌ برید. در این حالت، مسئله شما دیگه تعینی نیست و پیش‌بینی آینده یا پیش‌بینی مسیر، با عدم قطعیت (یا به عبارتی خطا) همراه خواهد بود. مثلا برای یک ولگرد نمی‌تونید با قطعیت کامل بگید که در فلان لحظه کجاست!

۲) علت حرکت چیزها

چیزها حرکت می‌کنند چون که بهشون نیرو وارد میشه! زمین دور خورشید می‌چرخه چون از طرف خورشید بهش نیرو وارد میشه یا توپ فوتبال حرکت می‌کنه چون یکی بهش ضربه می‌زنه! در مورد نور لامپ هم این جوری نیست که ما «کاری نمی‌کنیم»! در حقیقت با زدن کلید برق، جریان الکتریکی به لامپ میرسه و توی لامپ انرژی الکتریکی تبدیل به انرژی روشنایی میشه. یعنی همون‌جور که فوتبالیست به توپ ضربه می‌زنه و توپ حرکت می‌کنه، رسیدن جریان الکتریکی به لامپ‌ هم سبب ضربه زدن به نور میشه که به مسیرهای مختلف حرکت کنه. به این پدیده در فیزیک، تابش الکترومغناطیسی گفته میشه. به عبارت فنی‌تر، میدان الکتریکی اعمال شده توسط جریان خارجی (برق) سبب برانگیختگی ماده‌ای مثل تنگستن یا گاز خاصی مثل نئون میشه. برانگیختگی یعنی الکترون‌های که توی اتم‌های تشکیل دهنده اون مواد هستند از یک سطح انرژی به سطح بالاتری می‌رن (مثل وقتی که از پله‌های سرسره بالا میرین). اون موقع وقتی الکترون‌ها از یک سطح با انرژی بالاتر به سطی با انرژی پایین‌تر میان (مثل وقتی از سرسره پایین میاین)، اندازه اختلاف انرژی این دو سطح، از خودشون موج الکترومغناطیس یا ذرات نور منتشر می‌کنند!

این ویدیو رو ببینید:

۳) نور به دام سیاه‌چاله می‌افته؟

در مورد داستان سیاه‌چاله‌ها و اینکه چه‌طور از یک سیاه‌چاله میشه تصویر برداری کرد مفصل نوشتیم قبلا! این نوشته رو بخونید: قیام علیه سیاهی! به طور خلاصه، سیاه‌چاله‌ها اجسام بسیار بسیار سنگینی هستند که حتی بر حرکت نور هم اثر می‌ذارن. در مورد تصاویر منسوب به سیاه‌چاله‌ها هم، در حقیقت نوری که توی تصویر می‌بینیم دقیقا خود سیاهچاله نیست! یه سری موادی هستند که توی یه دیسک (شبیه حلقه‌های زحل) اطراف سیاهچاله دارن میچرخن و چون خیلی داغ هستن از خودشون نور تابش می‌کنن (درست شبیه به همون لامپ!). درواقع ما نور این موادی که در اطراف سیاهچاله وجود دارند و تونستن قسر دربرن و به چشم ما برسن رو می‌بینیم. تصویر ثبت شده، به خاطر اون نورها هست!

کمی توضیح فنی‌تر: ناحیه‌ای هست به‌اسم کره فوتونی که نزدیکترین مدار به افق رویداد که فوتون‌ها می‌تونن توی یه مدار پایدار دور سیاهچاله بچرخن. نزدیک‌تر از اون دیگه تقریبا فوتون شانسی برای برگشت نداره!

۴) آیا نور فقط سرعتش زیاده؟

نه! هر چیزی می‌تونه خیلی سریع حرکت کنه. محدودیتی در اصول نداریم. مثلا در آزمایش‌های مختلف فیزیکی، نوترون‌ها، الکترون‌ها یا پروتون‌ها رو با سرعت‌های خیلی زیاد به حرکت در میارن. یکی از جاهایی که مثلا پروتون‌ها رو تا سرعت‌های نزدیک به سرعت نور به حرکت در میارن آزمایشگاه سرن هست.

۵) آیا نور ثابته؟!

سوال رو درست متوجه نشدم! اگر منظور سرعت حرکت نوره، بله سرعت حرکت نور در هر محیط ثابته ولی موقعی که از محیطی به محیط دیگه میره تغییر میکنه. مثلا سرعت نور در هوا یک چیزه و در آب یک چیز دیگه‌ است. طبق نسبیت اینشتین، نور بیشترین سرعت در حرکت رو داره.

یک مقدمه اندوهناک

راستش را بخواهید نوشتن از این مسئله در همین شروع کار، برایم بسیار سخت به‌نظر می­رسد. حتی نمی‌­دانم باید از کجا شروع کنم. فکر کنم آخر آخرش چیزی بهتر از یک درد دل ساده به روال نق زدن‌­های معمول از آب در نیاید، اما نق زدن هم گاهی مفید است. دیگر کم کمش این است که آدم خالی می‌­شود. در کمدی الهی دانته می‌­خوانیم که: «ما به دنیا نیامدیم که مانند حیوانات زندگی کنیم، بلکه آمده‌­ایم تا علم و راه حق را دنبال کنیم.» جالب است که ادیبان بسیاری از فردوسی و سعدی و مرحوم شاملوی خودمان گرفته، تا گوته و دانته، همیشه به ضرورت نگرش علمی بشر پرداخته و از آن سخن­‌ها گفته‌­اند. نویسندگان بزرگی هم از راه رسیده‌­اند و دستاورد­های علمی را جان­‌مایه‌ی کارشان قرار داده‌اند و گاه بسیار الهام­‌بخش بوده‌­اند. چه برای کسانی که کار علمی می‌­کنند و چه برای کودکانی که جهان را با نگاه معصومانه و کنجکاوشان جستجو می­کنند. فکر می‌­کنم کودکی همه‌ی هم­‌نسلان ما و پدرانمان با نام ژول ورن عجیبن شده است. شکار شهاب، بیست هزار فرسنگ زیر دریا، سفر به ماه و یا سفر به مرکز زمین. مهم نبود که کتاب را بخوانید یا کارتون آن را در سیمای کودک شبکه یک نگاه کنید! به هر حال جذب زیبایی داستان و در واقع جذب هیجان سفر به جهان‌­های ناشناخته می‌­شدید.

حالا اینکه این چه ربطی به عنوان و درد دل­‌های من دارد، توضیح خواهم داد! از زمان پیدایش­مان بر این سیاره‌ی بی‌­نظیر، تلاش کردیم بهتر بفهمیم و بیشتر ببینیم. مطالعه‌ی طبیعت نیاز ما بوده و هست. هرچه محیط اطرافمان را بهتر شناختیم، با خطراتش بهتر و بیشتر آشنا شدیم و توانستیم منابع­ش را به نفع خودمان استخراج کنیم. از طرفی پس از گالیله و نیوتون، ابزار ریاضیات را به طور سیستماتیک برای مطالعه‌­مان بر روی طبیعت استفاده کرده­‌ایم. پس از دوران طلایی فیزیک، یعنی اواخر قرن نوزده و قرن بیست، دستاوردهای بزرگی بدست آوردیم که نه تنها عطش ما را برای دانستن ارضا نکرد، بلکه متوجه شدیم چقدر جهان ما عجیب‌­تر و مرموزتر از آن است که تصور می‌­کردیم. حالا با ابزار بی‌­نظیر ریاضیات، تجربه‌ی گذشتگان و تلاشی بی‌­وقفه به دنبال پاسخ سوالاتمان در حرکتیم. نظریات کوانتوم و نسبیت، یعنی دو دستاورد مهم و بزرگ ذهن بشر، دریچه‌ه­ایی از صدها سوال پیش رویمان گشوده‌اند. به لطف پیشرفت تکنولوژی، تا اعماق کیهان را رصد می‌­کنیم، دست‌­سازه­‌هایی به سیارات دیگری ازجمله مریخ، زحل و مشتری می‌فرستیم، ذرات با انرژی­‌های بالا را به‌هم برخورد می‌­دهیم و سعی می­‌کنیم نزدیک شویم به لحظات اولیه‌ی آفرینش (مه‌بانگ). چرا که هنوز می‌­خواهیم جهان­مان را بشناسیم. اینکه از کجا آمده‌­ایم؟ چرا وجود داریم؟ جهان­مان چه سرنوشتی خواهد داشت؟ ما، این موجودات کوچک، روی سیاره‌­ای کوچیک، ساخته شده از اتم­‌هایی که روزی در دل ستاره‌ای در کیهان گرم و کوچکتر از آنچه امروز هست تشکیل شده‌­اند، به کمک نیروی اندیشه به دنبال پاسخ این پرسش­‌هاییم. پس علم، این نیاز به دانستن ما را تا اینجا پیش آورده است. هنر هم دیگر نیاز مغز بشر را! ببینید چه زیبایی‌­هایی به این جهان اضافه کرده. مگر می‌­شود آن همه سمفونی و صدای زیبا، نقاشی­‌های بی‌نظیر و تابلو­های فرش را ندید؟

اندوه برای چه؟!

خب با این مقدمه‌ی طولانی بیایید برگردیم به موضوع اصلی. از صحبت‌­های بالا اینطور برداشت می‌­شود که خب پس همه چیز خوب و شاد است. اما نیست! هنر و علم در کنار یکدیگر ترکیب فوق‌­العاده‌­ای تشکیل داده­‌اند. اغلب ما با جنگ ستارگان خاطره داریم. نبرد بین امپراطوری کهکشان و این جور صحبت­‌های مهیج. لابد همه هم فیلم­های آدم فضایی­ها و جنگ دنیاها را دیده‌­ایم و کلی کیف کرده­‌ایم که یک عده بیگانه آمده‌­اند آدم­‌ها را نابود کنند و ما برای نجات سیاره­‌مان تلاش می‌­کنیم. خیلی هم قشنگ و خوب و شیرین است که ما، آدم­‌هایی که تا همان دو دقیقه قبل فیلم حتی سر یک بازی فوتبال بدترین ناسزاها را نثار هم می‌­کنیم، چه برسد به مسائل سیاسی و نفت و جنگ و فقر، در این فیلم‌­ها یک تنه از جان‌گذشتگی می‌کنیم برای نجات سیاره عزیزمان اما در پس ذهنمان می‌­دانیم که فعلا این چیزها هیچ حقیقتی ندارند و صرفا داریم سرگرم می‌­شویم. می‌­دانیم هیچ موجود فضایی تا کنون مشاهده نشده و ناسا کسی را در یخچال‌­هایش در زیر زمین زندانی نکرده و ما مورد حمله‌ی تمدن­‌های غریب نیستیم که بیایند خورشیدمان را بدزدند و ببرند. برای همین هم روی سخن هم اصلا این قسم فیلم‌­ها و کتاب­‌ها نیست. تازه بماند که شاهکارهایی نظیر «میان‌ستاره‌­ای» نولان، به یمن حضور کیپ تورن، از پایه‌ی علمی قویی هم برخوردارند.

درد چیست؟!

درد از آنجا ناشی می‌­شود که عده‌­ای به اسم ادیب، شاعر و یا نویسنده‌ی علمی، به قلمروهایی وارد می‌­شوند که ذره‌­ای تخصص در آن­ها ندارند. خیلی خوشبینانه می‌­شود فکر کرد که صرفا این زمینه‌­های علمی جذاب هستند و هرکسی دلش می‌­خواهد از سر سادگی درباره­‌شان نظر دهد و بنویسد. اما متاسفانه کار به همین یک نظر ساده دادن ختم نمی‌­شود. کانال‌­های تلگرامی، صفحات فیس‌­بوک و اینستاگرام، وبسایت­‌های متعدد و برخی مکان­‌ها در سطح شهر دست به کلاهبرداری علنی و آشکار به نام علم زده‌­اند، و از این راه بسیار پول‌دار هم شده­‌اند. از «اسرار کوانتومی اشرف مخلوقات» صحبت می­کنند، «عرفان­‌های کوانتومی» می‌­سازند و با علم کوانتوم می‌­خواهند افسردگی و روان‌­پریشی را درمان کنند. بسته­‌های درمانی-آموزشی درست کرده­‌اند و ماهیانه حراج­‌های استثنایی میگذارند. این کار کلاه­برداری و دزدی آشکار است. هرگز علم به چنین قلمروهایی وارد نشده است. این گروه‌­ها هرچه هستند و هرکه هستند، قصد و نیت­شان تنها فریب و پول درآوردن از راهی کاملا غیر قانونی(؟!) و غیر اخلاقی­ست. فیزیک کوانتومی حتی برای فیزیکدان‌­ها، هنوز پر از سوال و رمز و راز است. استفاده از دستور زبان سنگین علمی برای پول درآوردن و سود جویی چیزی جز شیادی نیست. گروه دیگری هم به قلمرو نسبیت و کیهان­‌شناسی و نجوم تاخته‌اند و در قرن بیست‌و‌یکم ادعا می‌­کنند که زمین تخت است. ناسا و تمام کشفیات رصدی به ما دروغ می‌­گویند. این‌­ها همه و همه توطئه‌ی غرب است تا ذهن­‌های ما را فاسد کند. حالا اینکه چه نفعی دارد یک کمپانی عظیم مانند ناسا عکس و فیلم­‌های تقلبی بسازد که مغز عده­‌ای را در یک کشور جهان‌سومی آن سوی جهان فاسد کند بماند. این عزیزان هم ادعا می­کنند اصلا ماهواره‌­ای ساخته نشده، جاذبه و نسبیت چرت است، زمین هم تخت است و همه در اشتباه محض هستند

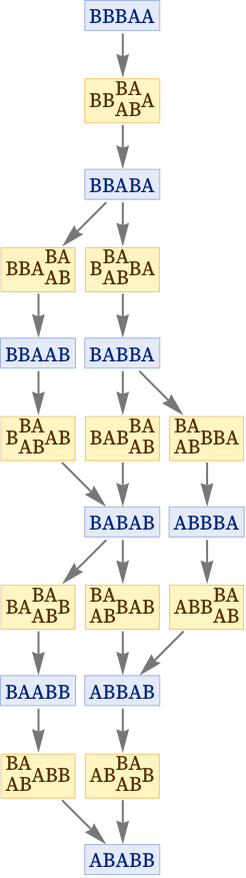
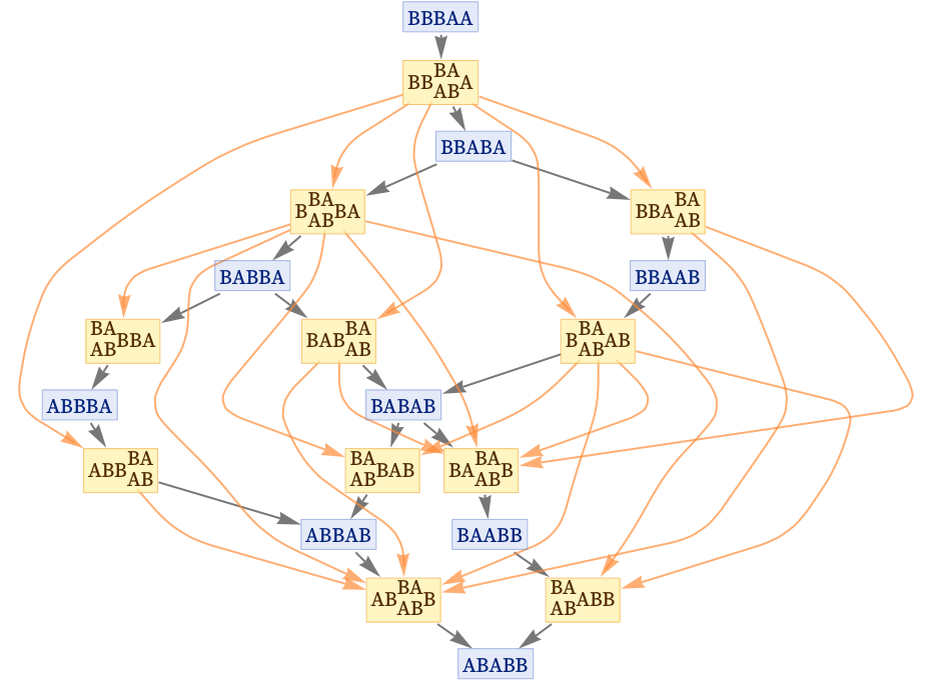
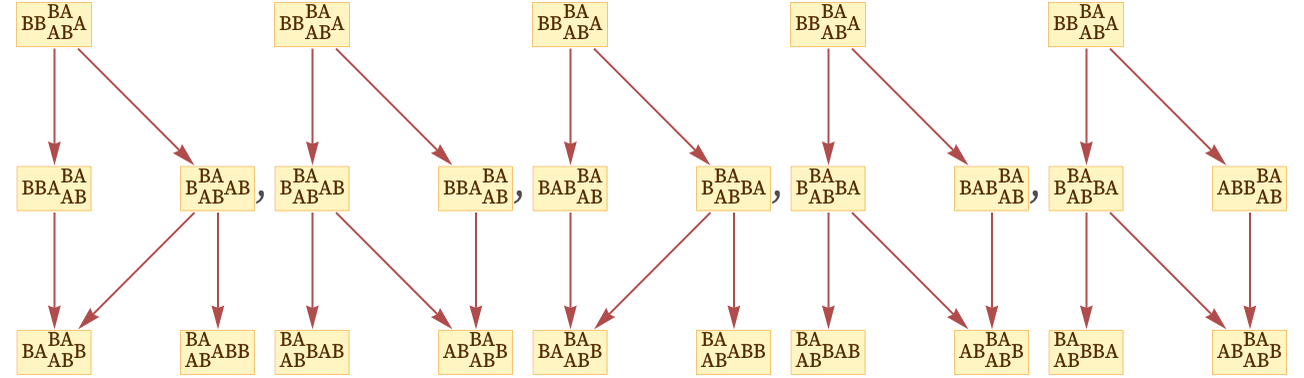
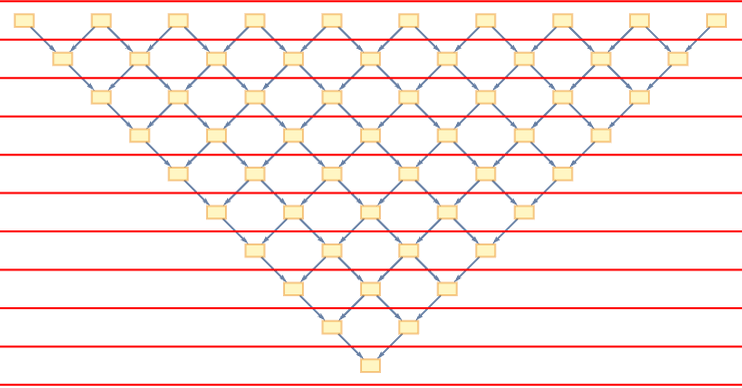
خب این هم یک نوعش است. اما یادمان باشد، برای مطرح کردن خود و یا پرپول کردن جیب‌­هایمان، دست به هر کاری نزنیم. یادمان باشد انسان‌­های بزرگی قرن­‌ها زحمت کشیده­‌اند. علم میوه‌ای نیست که یک شبه به ثمر رسیده باشد. یادمان باشد برای نفع شخصی، روی چه دستاورده‌ایی پا می‌­گذاریم. امروز در کشور ما، دانشجویان رشته­‌های علوم پایه و علوم انسانی، با سختی و مشقت زیاد شبانه‌­روز مطالعه می­‌کنند، بدون داشتن حتی ذره­‌ای امید برای داشتن شغلی با اندک حقوق در آینده. درست نیست با رواج این قسم خزعبلات، تنها امیدشان را با خاک یکسان کنیم. این گروه­‌ها از واژگان زیبای علمی استفاده می‌­کنند، اما مطالب غلطی را گسترش می‌­دهند. به همین دلیل، عنوان این نوشته را خرافه‌ی قرن بیست‌ویک گذاشتم. حقیقتا این مطالب با خرافات تفاوت چندانی ندارد. در جوامع خرافه‌باور با سطح مطالعه و اطلاعات بسیار کم، قطعا کار این انسان­‌ها راحت­‌تر و آسوده­‌تر خواهد بود. شدیدا خواندن کتاب «چرندیات پست مدرن» را به شما پیشنهاد می‌کنم! پیش از اینکه سخن پایانیم را بنویسم، پست اینستاگرامی دکتر فیروز نادری را اینجا به اشتراک می­گذارم که بسیار قابل تامل است؛

“Use your Heads — Don’t believe everything you read on Internet, YouTube, Telegram Channel or you hear in Masjed or from your cousin. You are more likely to die in a car crash than be hit by an asteroid on Feb 2019. HAARP is not the cause of Earthquakes in Iran or elsewhere. And, Moon landing was not faked and Earth is not flat and saints don’t live in wells.“

و اما سخن پایانی

می‌­شود به جای باور هر مزخرفی از جانب گروه­‌های معلوم‌­الحال، به کتابفروشی‌­ها رفت و کتاب­‌های علمی معتبر و خوبی که برای فهم عموم نوشته شده ‌است را تهیه کرد. حتی می‌­شود همان کتاب‌­ها را به صورت الکترونیکی هم تهیه کرد و از مطالعه‌­شان روی تبلت و گوشی هم لذت برد. می­شود مجلات علمی مانند نجوم و دانشمند و غیره را خرید و مطالعه کرد، تا هم از چنین موسسات علمی حمایت شود، هم اطلاعات معتبر علمی دریافت کرد. می‌­شود در سمینارها و سخنرانی‌­هایی که هر هفته در گوشه و کنار شهر برگزار می‌­شود استفاده کرد و … . امروز عصر ارتباطات است. پس بیایید اطلاعات معتبر و دقیق بگیریم، تفکر کنیم و از هر لحظه برای یادگیری استفاده کنیم. قطعا نتیجه برای خودمان، فرزندانمان و آینده‌ی مملکتمان درخشان­‌تر خواهد بود تا برای «عرفان کوانتومی» و «اسرار اشرف مخلوقات» و «زمین تخت گرایان». کشور ما قربانی قرن­‌ها خرافه است. بیایید با مطالعه، جلوی رشد این سرطان فکر را بگیریم. این بار هم به جای پایان دادن به نوشته‌­ام با جمله‌­ای از هاوکینگ، فاینمن، اینشتین و یا نیوتون، به نظرم خیلی بهتر است مخلص کلام را با این بیت فردوسی بیان کنم و این نق­نامه و درددل را تمام کنم:

ز دانش بِه اندر جهان هیچ نیست/ تن مرده و جانِ نادان یکی­ست